K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
25 tháng 12 2021
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Vẽ hình ghi gt và kl giúp em luôn nha
S
29 tháng 4 2019
a, xét tam giác CMA và tam giác BMD có : AM = MD (gt)
BM = CM do AM là trung tuyến (gt)
góc CMA = góc BMD (đối đỉnh)
=> tam giác CMA = tam giác BMD (c - g - c)
=> BD = AC (đn)
TV
Vẽ hình, GT và KL cho định lí hai góc cùng bù với một góc thú ba thì chúng bằng nhau
Nhớ vẽ hình nhé
1
3 tháng 10 2018
\(GT:\widehat{xOz}+\widehat{yOz}=180^o\)
\(\widehat{yOz}+\widehat{yOt}=180^o\)
\(KL:\widehat{xOz}=\widehat{yOt}\)
B
0
9 tháng 9 2018
giả thiết: 1 đường thẳng vuông góc với một trong 2 đường thẳng
kết luận: nó vuông góc với đường thẳng còn lại.
BẬT MÍ CHO BẠN NÈ: GIẢ THIẾT LÀ NHỮNG CHỮ Ở SAU TỪ ''NẾU''
KẾT LUẬN LÀ NHỮNG CHỮ SAU TỪ THÌ
AR
2
20 tháng 12 2021
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
AR
1
19 tháng 12 2021
a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC
AR
1
16 tháng 12 2021
1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.
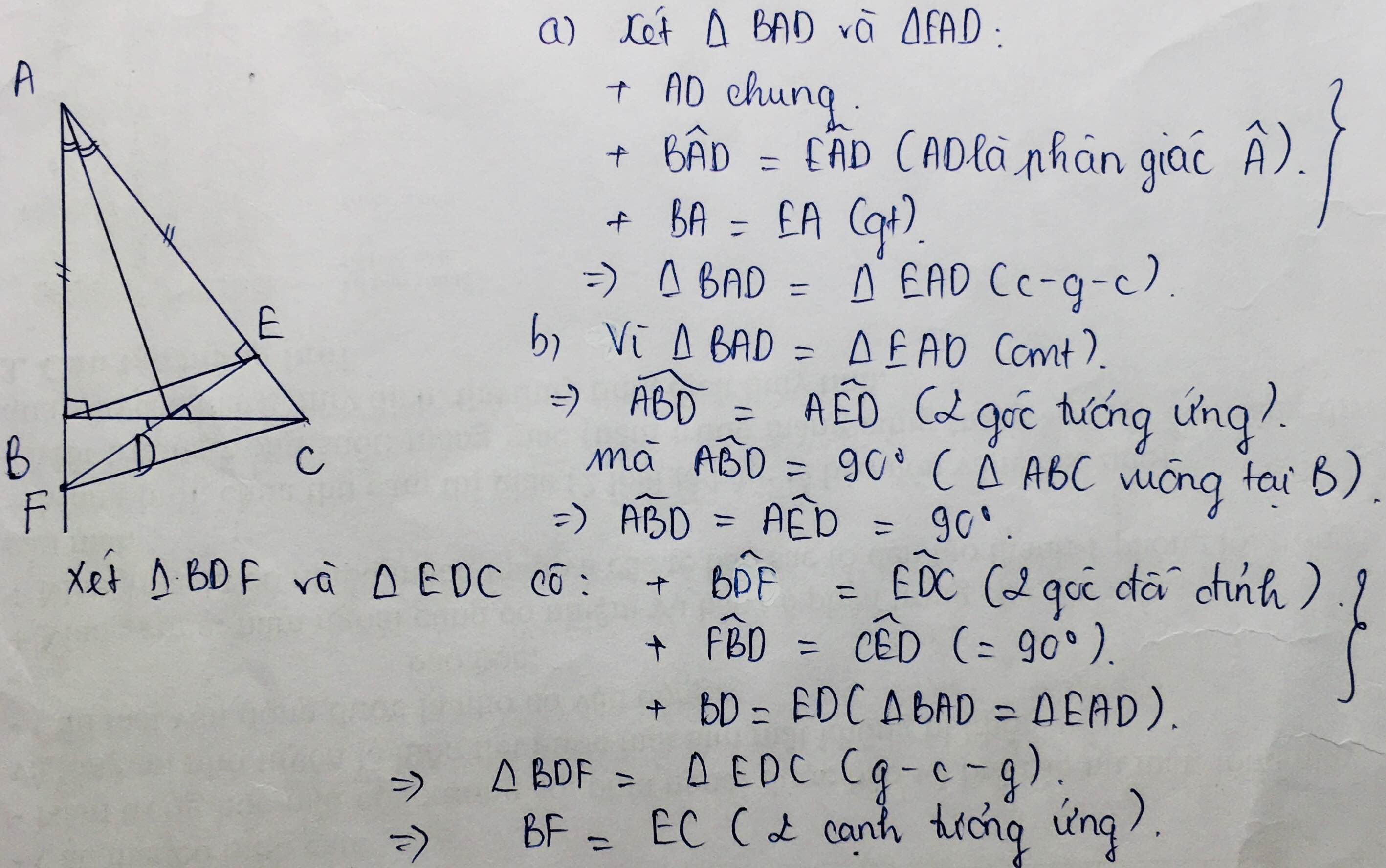
a: Ta có: a\(\perp\)c
b\(\perp\)c
Do đó: a//b
còn câu b nữa ạ