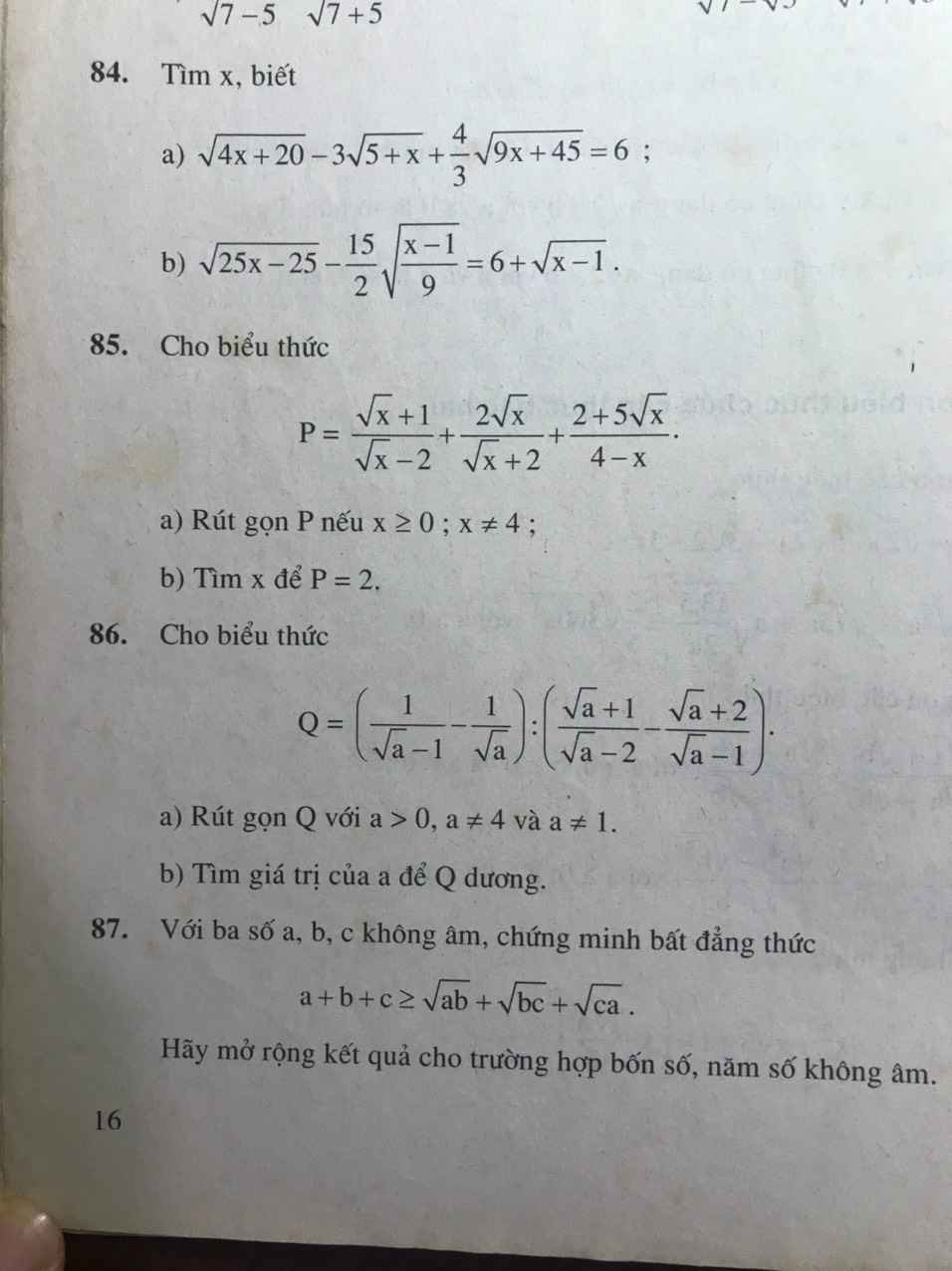K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
2
17 tháng 12 2020
Xét hiệu \(x^4-15x+14=\left(x-1\right)\left(x-2\right)\left(x^2+3x+7\right)\le0\)
\(\Rightarrow x^4\le15x-14\).
Tương tự: \(y^4\le15y-14;z^4\le15z-14\).
Cộng vế với vế của các bất đẳng thức trên kết hợp giả thiết x + y + z = 5 ta có:
\(P=x^4+y^4+z^4\le15\left(x+y+z\right)-42=33\).
Đẳng thức xảy ra khi và chỉ khi (x, y, z) = (2, 2, 1) và các hoán vị.
Vậy...
17 tháng 12 2020
cho mình hỏi làm thế nào để bạn tìm ra đc cách xét hiệu x4-15x+14
có phưong pháp nào ko
nếu có thì bn giúp mk vs nhé
22 tháng 8 2021
Bài 86:
a: Ta có: \(Q=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b: Để Q>0 thì \(\sqrt{a}-2>0\)
hay a>4
25 tháng 1 2022
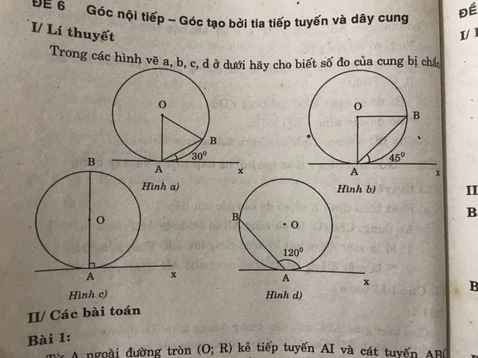
Hình a: 60 độ
Hình b: 90 độ
Hình c: 180 độ
Hình d: 120 độ
18 tháng 2 2022
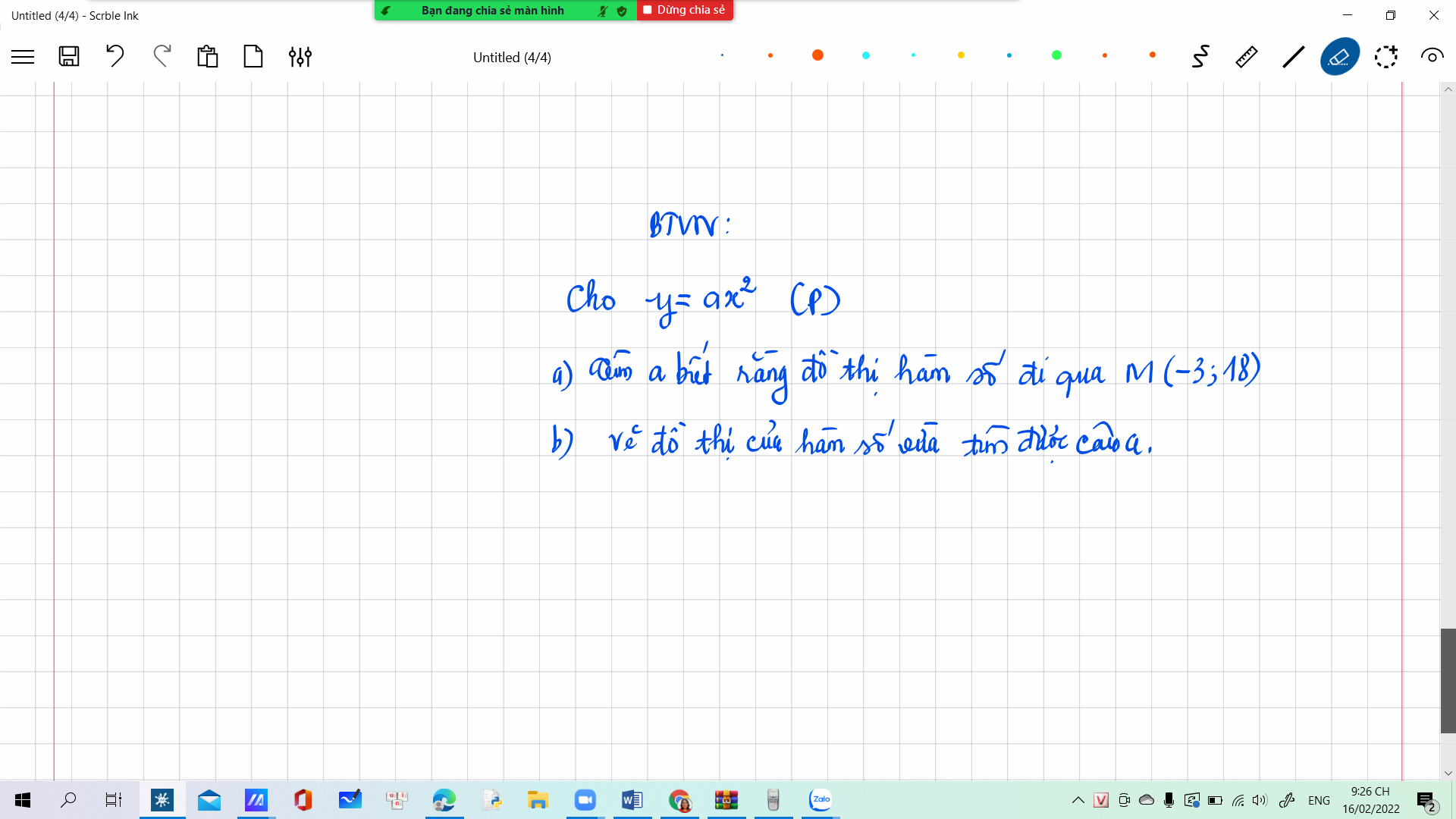
a, (P) đi qua M(-3;18)
<=> \(-18=9a\Leftrightarrow a=-2\)
Vậy với a = -2 thì (P) đi qua M(-3;18)
b, bạn tự vẽ
MB
1
20 tháng 10 2021
Câu 15:
Ta có: \(\sqrt{32x}+\sqrt{50x}-2\sqrt{8x}+\sqrt{18x}\)
\(=4\sqrt{2x}+5\sqrt{2x}-4\sqrt{2x}+3\sqrt{2x}\)
\(=8\sqrt{2x}\)
MB
3
20 tháng 10 2021
Câu 14 : \(C=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-\sqrt{x}}\right):\dfrac{1}{\sqrt{x}-1}\) với x >0 ; x≠0
\(C=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\dfrac{1}{\sqrt{x}-1}\)
\(C=\left(\dfrac{\sqrt{x}.\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{2}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\dfrac{1}{\sqrt{x}-1}\)
\(C=\dfrac{x+2}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\sqrt{x}-1}{1}\)
\(C=\dfrac{x+2}{\sqrt{x}}\)
Chúc bạn học tốt
MB
1
