Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

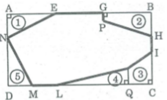
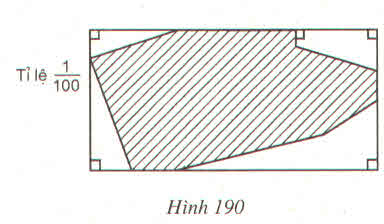
Giả sử hình chữ nhật là ABCD.
Trên AB, 2 giao điểm là E và G.
Trên BC hai giao điểm là I và H.
Trên CD hai giao điểm là L và M. Giao điểm trên AD là N. Hình thang tại đỉnh B có giao điểm là P, điểm trên đường gấp khúc IL là K.
Kẻ KQ ⊥ CD, gọi điện tích phẩn gạch đậm là S.
Ta có: S = S A B C - S A N E - S B H P G - S I C Q K - S D M N
Dùng thước chia khoảng đo các đoạn (mm):
AB, AD, AE, AN, PG, GB, BH, IC, CQ, QK, LQ, DM

Tỉ số giữa số thứ nhất và số thứ ba là: \(\dfrac{2}{3}.\dfrac{1}{4}=\dfrac{1}{6}\)

Vì mình chưa đc làm CTV nên kh đăng ảnh lên được , bạn thông cảm :

Bạn vào thống kê hỏi đáp mình là có ảnh nhé
Tham khảo thêm : https://lazi.vn/edu/exercise/406693/chung-minh-rang-neu-tam-giac-abc-dong-dang-voi-tam-giac-abc-theo-ti-so-k-thi-ti-so-cua-hai-duong-trung-tuyen-tuong-ung-cua-hai-tam
https://lazi.vn/edu/exercise/406693/chung-minh-rang-neu-tam-giac-abc-dong-dang-voi-tam-giac-abc-theo-ti-so-k-thi-ti-so-cua-hai-duong-trung-tuyen-tuong-ung-cua-hai-tam
Tham Khảo link trên nha bn

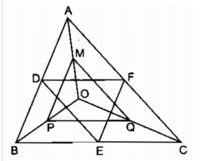
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 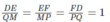
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.