Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi S là diện tích của thùng, h là chiều cao thì V = S.h. với V không đổi thì diện tích S và chiều cao h tỉ lệ nghịch với nhau.
\(\frac{h'}{h}=\frac{S}{S'}\)
(S' là diện tích đáy của thùng khi giảm chiều dai và chiều rộng 1,5 lần)
theo đề bài ta có: \(\frac{S}{S'}\)=2,25
(vì chiều dài và chiều rộng đều giảm 1,5 lần nên S giảm 1,5 x 1,5=2,25 lần)
do đó h'=2,25h
vậy chiều cao phải tăng thêm 2,25 lần

* Thể tích hình hộp chữ nhật V = S.h
Trong đó; S là diện tích đáy và h là chiều cao của hình hộp chữ nhật.
* Gọi chiều dài, chiều rộng và chiều cao của bể nước theo dự định ban đầu lần lượt là a, b và h (a, b, h > 0).
Khi giảm cả chiều dài và chiều rộng đáy bể đi 1,5 lần ta được chiều dài và chiều rộng mới là: 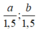
* Diện tích đáy bể theo dự định ban đầu là: S = ab.
Diện tích đáy bể sau khi thay đổi kích thước là: 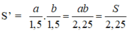
* Vì thể tích không đổi nên diện tích đáy bể và chiều cao là hai đaị lượng tỉ lệ nghịch nên ta có: S.h = S’.h’
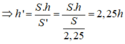
Vậy để thể tích bể không đổi thì chiều cao bể tăng gấp 2,25 lần so với dự định

Thể tích hình hộp chữ nhật V = S.h
Vì thể tích không đổi nên S và h là hai đại lượng tỉ lệ nghịch.
Diện tích đáy giảm: 1,5. 1,5 = 2,25 (lần)
Khi đó chiều cao h tăng thêm 2,25 lần.

Thể tích của 100 viên là:
100*2*1*0,5=100dm3
Diện tích đáy thùng là: 10^2=100dm2
Chiều cao của nước dâng lên là:
h=V/S=100/100=1dm
Mực nước trong thùng còn cách miệng:
10-1-5=4dm
