
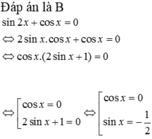
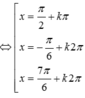

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

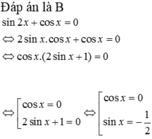
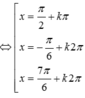


ĐK: \(x\ne\pm\dfrac{\pi}{4}+k2\pi\)
\(\dfrac{sin2x-1}{\sqrt{2}cosx-1}=0\)
\(\Leftrightarrow sin2x-1=0\)
\(\Leftrightarrow sin2x=1\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
Đối chiếu điều kiên ta được \(x=\pm\dfrac{3\pi}{4}+k2\pi\)


Hướng dẫn giải:
Chọn A.
![]() không là nghiệm của phương trình
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được - 3tanx + tan2x = 2(1+ tan2x)
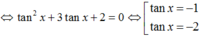
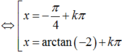

ĐKXĐ: x≠ \(k.\dfrac{\pi}{4}\) với k ∈ Z
Pt đã cho tương đương
\(\left\{{}\begin{matrix}sin4x.sin2x+sin4x.cosx=sin2x.cosx\\x\ne k\dfrac{\pi}{4}\end{matrix}\right.\)
Do x≠ \(k.\dfrac{\pi}{4}\) với k ∈ Z nên sin2x ≠ 0, chia cả 2 vế cho sin2x ta được
sin4x + 2cos2x.cosx = cosx
⇔ sin4x = cosx (1 - 2cos2x)
⇔ 4sinx.cosx.cos2x = cosx (1 - 2cos2x)
Do x≠ \(k.\dfrac{\pi}{4}\) với k ∈ Z nên cosx ≠ 0, chia cả 2 vế cho cosx ta được
4sinx.cos2x = 1 - 2cos2x
⇔ 4.sinx(1 - 2sin2x) = 1 - 2. (1- 2sin2x)
Đến đây tự giải kết hợp điều kiện nhé