K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
27 tháng 8 2018
Chọn A.
Từ giả thiết ta suy ra: (sinx+ cosx) 2 = ¼
Suy ra: 2sinx.cosx = -3/4 hay sinx.cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
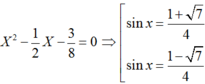
Do sinx + cosx = ½ nên 2(sinx + cosx) = 1
+) Với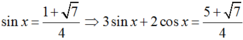 
+) Với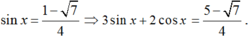 
18 tháng 7 2020
ĐK: x \(\ne\frac{\pi}{2}+k\pi\)
pt <=> \(3\sin x.\cos x+2\cos^2x=3\cos x+3\sin x-1\)
<=> \(3\sin x\left(\cos x-1\right)+\left(2\cos x-1\right)\left(\cos x-1\right)=0\)
<=> \(\left(\cos x-1\right)\left(3\sin+2\cos x-1\right)=0\)ok. Tự làm tiếp nha!
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2019
a/ \(sin3x=sin\left(2x+x\right)=sin2xcosx+cos2x.sinx\)
\(=2sinxcos^2x+\left(1-2sin^2x\right)sinx=2sinx\left(1-sin^2x\right)+sinx-2sin^3x\)
\(=3sinx-4sin^3x\)
b/
\(tan2x+\frac{1}{cos2x}=\frac{sin2x}{cos2x}+\frac{1}{cos2x}=\frac{sin2x+1}{cos2x}=\frac{2sinxcosx+sin^2x+cos^2x}{cos^2x-sin^2x}\)
\(=\frac{\left(sinx+cosx\right)^2}{\left(sinx+cosx\right)\left(cosx-sinx\right)}=\frac{sinx+cosx}{cosx-sinx}=\frac{\left(sinx+cosx\right)\left(cosx-sinx\right)}{\left(cos-sinx\right)^2}\)
\(=\frac{cos^2x-sin^2x}{cos^2x+sin^2x-2sinxcosx}=\frac{1-2sin^2x}{1-sin2x}\)
c/
\(\frac{cosx+sinx}{cosx-sinx}-\frac{cosx-sinx}{cosx+sinx}=\frac{\left(cosx+sinx\right)^2-\left(cosx-sinx\right)^2}{cos^2x-sin^2x}\)
\(=\frac{2sinxcosx+2sinxcosx}{cos2x}=\frac{4sinxcosx}{cos2x}=\frac{2sin2x}{cos2x}=2tan2x\)
d/
\(\frac{sin2x}{1+cos2x}=\frac{2sinxcosx}{1+2cos^2x-1}=\frac{2sinxcosx}{2cos^2x}=\frac{sinx}{cosx}=tanx\)
e/
5 tháng 5 2018
điều kiện : \(-1\le sinx;cosx\le1\)
ta có : \(sinx+cosx=\dfrac{1}{2}\Leftrightarrow cosx=\dfrac{1}{2}-sinx\)
ta lại có : \(sin^2x+cos^2x=1\Leftrightarrow sin^2x+\left(\dfrac{1}{2}-sinx\right)^2=1\)
\(\Leftrightarrow sin^2x+sin^2x-sinx+\dfrac{1}{4}=1\Leftrightarrow2sin^2x-sinx-\dfrac{3}{4}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=\dfrac{1+\sqrt{7}}{4}\\sinx=\dfrac{1-\sqrt{7}}{4}\end{matrix}\right.\)
ta có : (+) \(sinx=\dfrac{1+\sqrt{7}}{4}\Rightarrow cosx=\dfrac{1-\sqrt{7}}{4}\left(tmđk\right)\)
(+) \(sinx=\dfrac{1-\sqrt{7}}{4}\Rightarrow cos=\dfrac{1+\sqrt{7}}{4}\left(tmđk\right)\)
vậy ..........................................................................................................................
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2019
\(sin^8x-cos^8x-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-sin^2x\right)^4-4sin^6x+6sin^4x-4sin^2x\)
\(=sin^8x-\left(1-4sin^2x+6sin^4x-4sin^6x+sin^8x\right)-4sin^6x+6sin^4x-4sin^2x\)\(=-1\) (bạn chép nhầm đề)
b/ \(\frac{sin6x+sin2x+sin4x}{1+cos2x+cos4x}=\frac{2sin4x.cos2x+sin4x}{1+cos2x+2cos^22x-1}=\frac{sin4x\left(2cos2x+1\right)}{cos2x\left(2cos2x+1\right)}=\frac{sin4x}{cos2x}=\frac{2sin2x.cos2x}{cos2x}=2sin2x\)
c/ \(\frac{1+sin2x}{cosx+sinx}-\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}=\frac{sin^2x+cos^2x+2sinx.cosx}{cosx+sinx}-\left(1-tan^2\frac{x}{2}\right)cos^2\frac{x}{2}\)
\(=\frac{\left(sinx+cosx\right)^2}{sinx+cosx}-\left(cos^2\frac{x}{2}-sin^2\frac{x}{2}\right)=sinx+cosx-cosx=sinx\)
d/ \(cos4x+4cos2x+3=2cos^22x-1+4cos2x+3\)
\(=2\left(cos^22x+2cos2x+1\right)=2\left(cos2x+1\right)^2=2\left(2cos^2x-1+1\right)^2=8cos^4x\)
e/
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2020
\(M=sin^2x+cos^2x+2sinx.cosx+cos^2x-sin^2x\)
\(=\left(sinx+cosx\right)^2+\left(cosx-sinx\right)\left(cosx+sinx\right)\)
\(=\left(sinx+cosx\right)\left(sinx+cosx+cosx-sinx\right)\)
\(=2cosx\left(sinx+cosx\right)\)
\(=2\sqrt{2}cosx.cos\left(x-\frac{\pi}{4}\right)\)
H
1
11 tháng 8 2015
Biến đổi pt trên như sau:
sinx.cosx/4 + cosx.sinx/4 - 3(sin2x + cos2x) + cosx = 0
sin(x + x/4) + cosx = 3
sin5x/4 + cosx = 3
Vì sin5x/4 \(\le\) 1 và cosx \(\le\) 1. Do đó sin5x/4 + cosx \(\le\) 2. Vì vậy pt trên vô nghiệm.
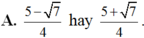
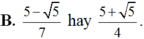
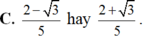
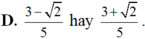
Chọn A.
Ta có:
sinx + cosx = ½ nên ( sinx + cosx)2 = ¼
Do đó sinx. cosx = -3/8
Khi đó sinx; cosx là nghiệm của phương trình
Ta có sinx + cos x = ½ nên 2( sinx + cosx) = 1
+) Với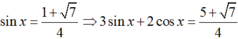
+) Với