Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi chiều rộng đáy của thùng hàng là x (x>0)
Chiều dài: \(\dfrac{3}{2}x\)
Chiều cao: \(\dfrac{15}{x.\dfrac{3}{2}x}=\dfrac{10}{x^2}\)
Diện tích đáy : \(\dfrac{3}{2}x^2\)
Diện tích mặt bên: \(2x.\dfrac{10}{x^2}+3x.\dfrac{10}{x^2}=\dfrac{50}{x}\)
Tổng chi phí: \(f\left(x\right)=10.\dfrac{3}{2}x^2+6.\dfrac{50}{x}=15x^2+\dfrac{300}{x}\)
\(f\left(x\right)=15\left(x^2+\dfrac{20}{x}\right)=15\left(x^2+\dfrac{10}{x}+\dfrac{10}{x}\right)\ge15.3\sqrt[3]{\dfrac{100x^2}{x^2}}\simeq209\left(USD\right)\)
Bạn tính toán lại

Đáp án là C
Gọi chiều rộng của đáy là x (cm) (x > 0)
Khi đó chiều cao của hố ga là 2x và chiều dài của hố ga là 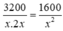
Diện tích xung quanh hố ga là 
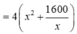
Diện đáy của hố ga là 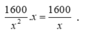
Tổng diện tích xây hố ga đó là 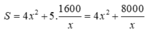
Để xây tiết kiệm nguyên vật liệu nhất thì S phải nhỏ nhất.
Áp dụng bất đẳng thức Cô-Si ta có
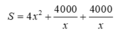
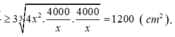
Dấu bằng xảy ra khi và chỉ khi ![]()
Khi đó diện tích đáy của hố ga là 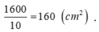

Chọn B
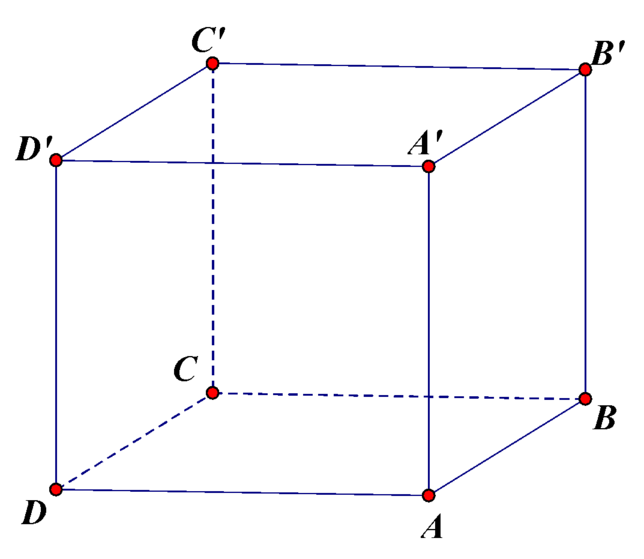
Giả sử khối hộp chữ nhật là ![]() và
và ![]() ,
, ![]() và
và ![]() (
(![]() ).
).
Ta có ![]()
![]()
![]() .
.
Diện tích cần xây là ![]()
![]() .
.
Ta cần tìm giá trị nhỏ nhất của ![]() với
với ![]() .
.
Ta có ![]()
![]() .
.
Dấu đẳng thức xảy ra khi![]()
![]() .
.
![]() nhỏ nhất là
nhỏ nhất là ![]() khi
khi ![]() .
.
Số tiền chi phí là ![]() hay
hay ![]() triệu đồng.
triệu đồng.
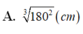
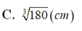
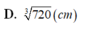


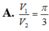


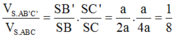
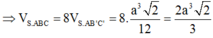




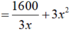

Chọn C.
Đáy có kích thước là x, 3x
Chiều cao là z nên thể tích thùng là
Để tốn ít vật liệu nhât thì diện tich sản xuất phải nhỏ nhất.
Dấu bằng xảy ra khi và chỉ khi
Khi đó