Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: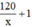 
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: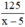 
(h)
Theo bài ra ta có phương trình:
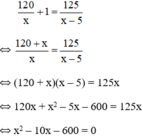
Có a = 1; b = -10; c = -600 ⇒ Δ’ = (-5)2 – 1.(-600) = 625
Phương trình có hai nghiệm phân biệt:
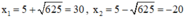
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.
Gọi vận tốc của xuồng lúc đi là x (km/h, x > 5).
⇒ Vận tốc của xuồng lúc về là x – 5 (km/h).
Thời gian đi là: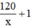 
(h)
Quãng đường về là: 120 + 5 = 125 km
Thời gian về là: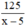 
(h)
Theo bài ra ta có phương trình:
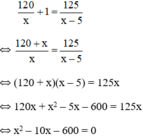
Có a = 1; b = -10; c = -600 ⇒ Δ ’ = ( - 5 ) 2 – 1 . ( - 600 ) = 625
Phương trình có hai nghiệm phân biệt:
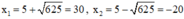
Trong hai nghiệm chỉ có nghiệm x = 30 thỏa mãn điều kiện.
Vậy vận tốc xuồng lúc đi là 30 km/h.
Kiến thức áp dụng
Để giải bài toán bằng cách lập phương trình ta làm theo các bước:
Bước 1: Lập phương trình
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu diễn tất cả các đại lượng khác qua ẩn vừa chọn.
+ Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình
Bước 3: Đối chiếu điều kiện rồi kết luận.
*Gọi vận tốc riêng của thuyền là x (km/h) (1<x < 60)
Vận tốc khi xuồng xuôi dòng là: x + 1 (km/h)
Vận tốc khi xuồng ngược dòng là: x - 1(km/h)
*Thời gian xuồng xuôi dòng từ A --> B là: 60/(x + 1) (h)
Thời gian xuồng xuôi dòng đến bến C là: 25/(x - 1) (h)
30 phút = 1/2 (h)
*Vì thời gian kể từ lúc đi đến lúc quay trở lại đến bến C hết tất cả là 8 giờ nên ta có PT:
60/(x + 1) + 25/(x - 1) + 1/2 = 8
=> 60.2.(x - 1) + 25.2(x + 1) + (x - 1)(x + 1) = 8.2(x - 1)(x + 1)
<=> 120x - 120 + 50x + 50 + x^2 - 1 = 16x^2 - 16
<=> 15x^2 - 170x + 55 = 0
delta' = (- 85)^2 - 55.15 = 6400 = 80^2 > 0
=> PT có 2 nghiệm pb:
x1 = (85 - 80)/15 = 1/3 (loại)
x2 = (85 + 80)/15 = 11 (thỏa mãn điều kiện bài ra)
Vậy vận tốc xuồng máy khi nước yên lặng là 11km/h
bài 41
:
Gọi x là số mà một bạn (Minh hoặc Lan) đã chọn và số mà bạn kia chọn là x + 5.
Khi đó tích của hai số là x(x+5).
Theo đề bài ta có phương trình x(x+ 5) = 150
Vậy:
Nếu bạn Minh chọn số 10 thì bạn Lan chọn số 15 hoặc ngược lại.
Nếu bạn Minh chọn số -15 thì bạn Lan chọn số -10 hoặc ngược lại.
bài 42:
Gọi lãi suất cho vay là x (%), x > 0
Tiền lãi sau một năm là: 2 000 000 . x/100 hay 20000x (đồng)
Sau 1 năm cả vốn lẫn lãi sẽ là: 2 000 000 + 20000x (đồng)
Tiền lãi riêng năm thứ hai phải chịu là:
(2 000 000 + 20000x) x/100
hay 20000x + 200x2
Số tiền sau hai năm bác Thời phải trả là:
2 000 000 + 40000x + 200x2
Theo đầu bài ra ta có phương trình:
2 000 000 + 40 000x + 200x2 = 2 420 000 hay x2 + 200x – 2 100 = 0
Giải phương trình:
∆’ = 1002 – 1 . (-2 100) = 10 000 + 2 100 = 12 100
=> √∆’ = 110
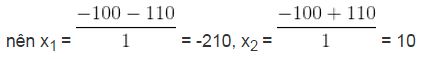
Vì x > 0 nên x1 không thỏa mãn điều kiện của ẩn.
Trả lời: lãi suất là 10%.
bài 43;
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vận tốc lúc về là x – 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là:
120/x + 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
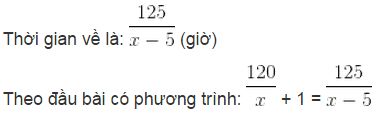
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h.
.
còn bài nào gửi lên mình trả lời cho.
`Gọi vận tốc của xuồng máy khi đi trong hồ yên lặng là \(x\) (km/h), \(x>3\)
Vận tốc của xuồng khi đi xuôi dòng sông là : \(x+3\) (km/h)
Vận tốc của xuồng khi đi ngược dòng sông là : \(x-3\) (km/h)
Khoảng cách giữa hai bến sông A và B là 60km. Một xuồng máy đi xuôi dòng từ A đến B nghỉ 30 phút tại bến B rồi quay trở lại đi ngược dòng 25km để đến bến C. Thời gian kể từ lúc đi đến lúc quay trở lại đến bến C là hết tất cả 8 giờ. Biết rằng vận tốc nước chảy là 1km/h.
Vậy vận tốc xuồng máy khi nước yên lặng là ............. km/h.
Để đường thẳng y = ax đi qua giao điểm của hai đường thẳng 2x - 3y = 8 và 7x - 5y = -5 thì giá trị của a là ............
Câu hỏi tương tự Đọc thêm
Toán lớp 9Violympic
Khoảng cách giữa hai bến sông A và B là 60km. Một xuồng máy đi xuôi dòng từ A đến B nghỉ 30 phút tại bến B rồi quay trở lại đi ngược dòng 25km để đến bến C. Thời gian kể từ lúc đi đến lúc quay trở lại đến bến C là hết tất cả 8 giờ. Biết rằng vận tốc nước chảy là 1km/h.
Vậy vận tốc xuồng máy khi nước yên lặng là ............. km/h.
Để đường thẳng y = ax đi qua giao điểm của hai đường thẳng 2x - 3y = 8 và 7x - 5y = -5 thì giá trị của a là ............
Câu hỏi tương tự Đọc thêm
Toán lớp 9Violympic
ai tích mình tích lại
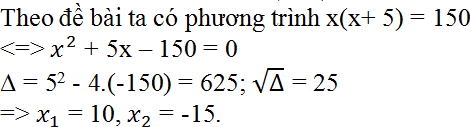
Gọi vận tốc của xuồng lúc đi là x (km/h), x > 0, thì vân tốc lúc về là x - 5 (km/h).
Vì khi đi có nghỉ 1 giờ nên thời gian khi đi hết tất cả là: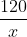
+ 1 (giờ)
Đường về dài: 120 + 5 = 125 (km)
Thời gian về là: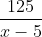
(giờ)
Theo đầu bài có phương trình: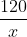
+ 1 =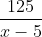 
Giải phương trình:
x2 – 5x + 120x – 600 = 125x ⇔ x2 – 10x – 600 = 0
∆’ = (-5)2 – 1 . (-600) = 625, √∆’ = 25
x1 = 5 – 25 = -20, x2 = 5 + 25 = 30
Vì x > 0 nên x1 = -20 không thỏa mãn điều kiện của ẩn.
Trả lời: Vận tốc của xuồng khi đi là 30 km/h
Bài 43 (SGK trang 58)
Một xuồng du lịch đi từ thành phố Cà Mau đến Đất Mũi theo một đường sông dài 120 km. Trên đường đi, xuồng có nghỉ lại 1 giờ ở thị trấn Năm Căn. Khi về, xuồng đi theo đường khác dài hơn đường lúc đi 5 km và với vận tốc nhỏ hơn vận tốc lúc đi là 5 km/h. Tính vận tốc của xuồng lúc đi, biết rằng thời gian về bằng thời gian đi.
Gọi x là vận tốc lúc xuồng đi(km/h, x > 5)
thì Vận tốc lúc về sẽ là x - 5 (km/h)
Tính cả 1 giờ nghỉ ở Năm Căn thì thời gian đi từ thành phố Cà Mau đến Đất Mũi là 120x + 1 (giờ)
Quãng đường lúc về dài: 120 + 5 = 125 (km)
Thời gian đi về hết: 125x−5 (giờ)
Theo đề bài ta có phương trình:
120x + 1 = 125x−5 <=> 120(x - 5) + x(x - 5) = 125x <=> 120x - 600 + x2 - 5x - 125x = 0 <=> x2 - 10x - 600 = 0
Giải phương trình x2 - 10x - 600 = 0
Δ′ = (−5)2 - 1.(-600) = 25 + 600 = 625
√Δ′ = √625 = 25
Phương trình có hai nghiệm x1 = -(-5) + 25 = 30, x2 = -(-5) - 25 = -20
Vì x > 5 nên ta chỉ chọn giá trị x1
Vậy vận tốc xuồng lúc đi là 30 (km/h)