Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc của xe máy là x (km/h; x > 0)
Vận tốc của ô tô là x + 24 (km/h)
Thời gian xe máy đi hết quãng đường là: 120/x (h)
Thời gian ô tô đi hết quãng đường là: 120/(x+4) (h)
Đổi 30 phút = 1/2 (h), 20 phút = 1/3 (h)
Theo đề bài ta có phương trình:
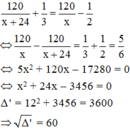
Phương trình có hai nghiệm x 1 = − 12 – 60 = −72 (loại) và x 2 = −12 + 60 = 48 (tmđk)
Vậy vận tốc xe máy là 48 km/h và vận tốc ô tô là 48 + 24 = 72 km/h
Đáp án: D

Gọi vận tốc ô tô là: x ( km/h ) ( x > 24 )
=) vận tốc xe máy là: x - 24 ( km/h )
Thời gian để ô tô đi hết quãng đường AB là: \(\frac{120}{x}\)( giờ )
Thời gian đẻ xe máy đi hết quãng đường AB là: \(\frac{120}{x-24}\)( giờ )
VÌ ô tô đến B được \(\frac{4}{3}\)giờ thì xe máy mới đén A cũng như ô tô đi trươc xe máy \(\frac{1}{2}\)giờ nên ta có phương trình:
\(\frac{120}{x-24}-\frac{4}{3}=\frac{120}{x}-\frac{1}{2}\)
\(\frac{120}{x-24}-\frac{120}{x}=\frac{5}{6}\)
\(\frac{720x}{6x.\left(x-24\right)}-\frac{720.\left(x-24\right)}{6x.\left(x-24\right)}=\frac{5x.\left(x-24\right)}{6x.\left(x-24\right)}\)
\(720x-720+17280=5x^2-120x\)
\(5x^2-120x-17280=0\)
\(x^2-24x-3456=0\)
\(\left(x-72\right).\left(x+48\right)=0\)
\(\orbr{\begin{cases}x=72\\x=-48\left(lo\text{ại}\right)\end{cases}}\)
Vận tốc ô tô là: 72 km/h
Vận tốc xe máy là: 48 km/h
Gọi vận tốc xe máy là x (km/h) (x>0)
thì vận tốc ô tô là: x + 24 (km/h)
Thời gian xe máy đi quãng đường AB là: \(\frac{120}{x}\)(h)
Thời gian ô tô đi quãng đường AB là:\(\frac{120}{x+24}\)(h)
Thời gian xe máy đi nhiều hơn ô tô: 1h20' - (7h30' - 7h) = 50' = \(\frac{5}{6}\) (h)
Ta có phương trình: \(\frac{120}{x}-\frac{120}{x+24}=\frac{5}{6}\)
<=> 6.[120(x+24) - 120x] = 5x(x+24)
<=> 720(x+24) - 720x = 5x^2 + 120x
<=> 5x^2 + 120x - 17280 = 0
<=> x = 48 (TMĐK) hoặc x = -72 (không TMĐK)
Vậy vận tốc xe máy là 48 km/h
vận tốc ô tô là: 48+24=72 (km/h)

Lời giải:
Gọi vận tốc xe máy là $a$ km/h thì vận tốc ô tô là $a+12$ km/h
Khi ô tô đi được 2 giờ thì xe máy đi được 3 giờ.
Quãng đường xe máy đi được cho đến khi gặp nhau: $3a$ (km)
Quãng đường ô tô đi được cho đến khi gặp nhau: $2(a+12)$ (km)
Tổng quãng đường 2 xe đi được cho đến khi gặp nhau chính là quãng đường $AB$
Do đó:
$AB=3a+2(a+12)$
$\Leftrightarrow 204=5a+24\Rightarrow a=36$ (km/h)
Vậy vận tốc xe máy là $36$ km/h

Gọi vận tốc trung bình của ô tô là x
Sau 3h xe máy đi được 3(x-10)(km)
theo đề, ta có:
(3x-30+30)/(x-10)=30/x
=>3x/(x-10)=30/x
=>3x^2=30x-300
=>x^2-10x+100=0
=>Ko có vận tốc của ô tô thỏa mãn

Gọi C là điểm của hai xe gặp nhau.
Gọi vận tốc xe máy là v thì vận tốc ô tô là v + 20 (đơn vị: km/h).
Trong 1h xe máy đi được: s=v.1=v(km)
Thời gian kể từ khi ô tô đi để hai xe gặp nhau là: \(t_0=\frac{s}{\left(v+20\right)-v}=\frac{s}{20}=\frac{v}{20}\left(h\right)\)
Quãng đường AC là: sAC=\(t_0.\left(v+20\right)=\frac{v}{20}.\left(v+20\right)=\frac{v^2}{20}+v\)\(\left(h\right)\)
Quãng đường CB là: sBC=sAB−sAC=\(210-\left(\frac{v^2}{20}+v\right)\left(km\right)\)Thời gian để ô tô đi quãng đường CB là: t=sBC\(:\left(v+20\right)=\left[210-\left(\frac{v^2}{20}\right)\right]\)\(:\left(v+20\right)\left(h\right)\)
Mà theo bài ra t = 1,5 (h)
Do đó \(\left[210-\left(\frac{v^2}{20}+v\right)\right]:\left(v+20\right)=1,5\)
⇔\(210-\left(\frac{v^2}{20}+v\right)=1,5v+30\)
⇔\(\frac{v^2}{20}+2,5v=180\)
⇔v2+50v=3600
⇔(v+25)2=4225
⇔v=40 (vì v > 0)
Do đó vận tốc xe máy là 40 (km/h)
Vận tốc ô tô là 60 (km/h)
Gọi vận tốc xe máy là x(km/h) và vận tốc xe ô tô là y(km/h)
Đk x,y>0 Đổi: 30 phút=0,5 h; 1h30 phút=1,5 h
Quãng đường xe máy đi là (0,5+1,5)x
Quãng đường xe ô tô đi là 1,5y
theo đề bài ta có
\(\left\{{}\begin{matrix}\text{(0,5+1,5)x}+1,5y=120\\y-x=10\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}\text{2x}+1,5y=120\\-x+y=10\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=30\\y=40\end{matrix}\right.\)(TMĐK)
Vậy ....
Gọi \(x\left(km/h\right)\) là vận tốc của xe máy \(\left(x>0\right)\)
\(y\left(km/h\right)\) là vận tốc của ô tô \(\left(y>10\right)\)
Vì vận tốc của ô tô lớn hơn vận tốc xe máy $10km/h$ nên ta có pt:
\(y-x=10\\ \Leftrightarrow-x+y=10\left(1\right)\)
Thời gian xe máy đi là: \(1,5+0,5=2\left(h\right)\)
Quãng đường xe máy đi là: \(2x\left(km\right)\)
Quãng đường ô tô đi là: \(1,5y\left(km\right)\)
Vì ô tô đi được 1h30 phút thì gặp xe máy nên ta cos pt:
\(2x+1,5y=120\left(2\right)\)
Từ $(1)&(2)$ ta có hệ phương trình $\begin{cases} -x+y=10 \\ 2x+1,5y=120 \end{cases}$
Giải hpt ta được $\begin{cases} x=30 \\ y=40 \end{cases} \text{(nhận)}$
Vậy ...