Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án A
Áp dụng định luật bảo toàn động lượng: m v = ( m + 2 m ) V ⇒ V = v 3
Chú ý: Va cham ở bài toán trên là va chạm mềm
Đáp án D
Gọi V là vận tốc của hai vật dính vào nhau sau khi va chạm mềm. Áp dụng định luật bảo toàn động lượng
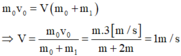
Đáp án A
Vận tốc của hệ hai vật sau khi va chạm
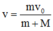
= 0,4 m/s
Quá trình va chạm không làm thay đổi vị trí cân bằng của hệ
→ v = v m a x
→ Biên độ dao động mới
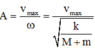
= 5cm
Đáp án C
+ Khi vật tới biên dưới, vật nhỏ tới va chạm và dính vào nên ta áp dụng bảo toàn động lượng ta có:
mv = (M + m).V ®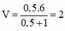 
m/s = 200 cm/s.
+ Vị trí cân bằng mới cách vị trí cân bằng cũ 1 đoạn là: 
m = 2,5 cm.
® Sau va chạm li độ của vật so với VTCB mới là: x 0 = A - x = 10 cm
+ Biên độ dao động mới của vật là:
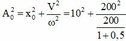
® A 0 = 20 cm.
Đáp án D
Va chạm là va chạm mềm nên tại vị trí va chạm: v 0 = m . v M + m = v 3 = 2 m / s
Vị trí cân bằng mới của con lắc cách vị trí cân bằng cũ 1 đoạn
OO ' = mg k = 0 , 5 .10 200 = 0 , 025 m = 2 , 5 cm
Ngay sau va chạm con lắc ở vị trí:
x ' = x − OO ' = A − OO ' = 10 cm v ' = v 3 ω ' = k m + M = 200 0 , 5 + 1 = 20 3 rad / s
Biên độ của con lắc sau va chạm:
A ' 2 = x ' 2 + v ' 2 ω 2 ⇔ A ' 2 = 10 2 + 200 2 20 3 2 = 400 ⇒ A ' = 20 cm
Đáp án C
Tốc độ của hệ sau va chạm:
Tần số góc:
→ 
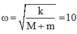
Biên độ: 
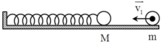
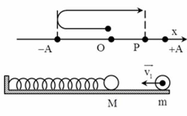
Thời điểm lò xo dãn 8 cm lần thứ nhất là khi vật đang ở vị trí P
= 0,41s
Đáp án B
Áp dụng định luật bảo toàn động lượng đối với hệ vật trước và sau khi va chạm ta có: