Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
? Lời giải:
− Trọng lực tác dụng lên vật: p = mg = 10 N
− Lực gây ra gia tốc a: F = ma = 5 N → f = P/2

Hình 21.3Ga
Phương trình chuyển động của vật trên các trục Ox, Oy là
Ox: Psina = ma (1)
Oy : N - Pcosa = 0 (2)
Mặt khác, theo bài ra : a = 2s/ t 2 (3)
Từ (1), (2) và (3) suy ra sin α = a/g = 2s/(g t 2 ) = 2.2,45/(9,8.1) = 0,5
⇒ α = 30 °

Áp dụng công thức về độ biến thiên động năng:
m v 2 /2 - m v 0 2 /2 = A = Fs
Với v 0 = 0 và F = Psin α - F m s = mg(sin α - μ cos α )
Từ đó suy ra:

Thay số, ta tìm được vận tốc của vật ở chân mặt phẳng nghiêng:
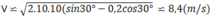

Độ lớn trọng lượng của vật P = mg = 4.10 = 40 (N)
Suy ra F/P = 8/40 = 1/5, lực gây ra gia tốc nhỏ hơn trọng lượng của vật 5 lần

\(\left\{{}\begin{matrix}Ox:mg\sin\alpha-F_{ms}=m.a\\Oy:N=mg\cos\alpha\end{matrix}\right.\Rightarrow mg\sin\alpha-\mu mg\cos\alpha=ma\)
\(\Rightarrow a=g\sin\alpha-\mu g\cos\alpha=...\left(m/s^2\right)\)

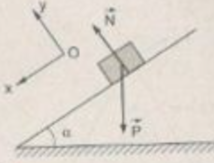
Phân tích lực theo 2 phương Ox: song song với mp nghiêng, chiều dương hướng xuống
Oy: vuông góc với mp nghiêng, chiều dương hướng lên
\(l=h.\sin\alpha=10\sqrt{2}.\dfrac{\sqrt{2}}{2}=10\left(m\right)\)
\(\left\{{}\begin{matrix}Ox:P\cos\alpha-F_{ms}=ma\\Oy:P\sin\alpha=N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}mg\cos\alpha-\mu N=m.a\\N=P\sin\alpha\end{matrix}\right.\Leftrightarrow g\cos\alpha-\mu g\sin\alpha=a=...\left(m/s^2\right)\)
b/ \(v^2-v_0^2=2aS\Leftrightarrow v=\sqrt{2.a.l}=...\left(m/s\right)\)
c/ \(t=\dfrac{v-v_0}{a}=\dfrac{v}{a}=...\left(s\right)\)
d/ \(l'=h'\sin\alpha=2\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\left(m\right)\)
\(v'^2=2aS\Rightarrow v=\sqrt{2.a.l'}=...\left(m/s\right)\)

Đáp án:
a.a=2,167m/s2b.v=1,862m/sc.t=0,86sd.a′=−2m/s2e.s′=0,8668mf.t′=0,931sa.a=2,167m/s2b.v=1,862m/sc.t=0,86sd.a′=−2m/s2e.s′=0,8668mf.t′=0,931s
Giải thích các bước giải:
a.
Ta có:
sinα=0,82=0,4cosα=√1−sin2α=√1−0,42=√215sinα=0,82=0,4cosα=1−sin2α=1−0,42=215
Áp dụng định luật II Niu tơn:
⃗P+⃗Fms+⃗N=m⃗a+oy:N=Pcosα+ox:Psinα−Fms=ma⇒a=Psinα−Fmsm=mgsinα−μmgcosαm=gsinα−μgcosα=10.0,4−0,2.10.√214=2,167m/s2P→+F→ms+N→=ma→+oy:N=Pcosα+ox:Psinα−Fms=ma⇒a=Psinα−Fmsm=mgsinα−μmgcosαm=gsinα−μgcosα=10.0,4−0,2.10.214=2,167m/s2
b.
Vận tốc tại chân mặt phẳng nghiêng là:
v2−v20=2as⇒v=√v20+2as=√0+2.2,167.0,8=1,862m/sv2−v02=2as⇒v=v02+2as=0+2.2,167.0,8=1,862m/s
c.
Thời gian chuyển động trên mặt phẳng nghiêng là:
t=v−v0a=1,862−02,167=0,86st=v−v0a=1,862−02,167=0,86s
d.
Áp dụng định luật II Niu tơn:
⃗P+⃗Fms+⃗N=m⃗a′+oy:N=P+ox:−Fms=ma′⇒a′=−Fmsm=−μmgm=−μg=−0,2.10=−2m/s2P→+F→ms+N→=ma→′+oy:N=P+ox:−Fms=ma′⇒a′=−Fmsm=−μmgm=−μg=−0,2.10=−2m/s2
e.
Quảng đường tối đa đi được trên mặt phẳng ngang là:
s′=v′2−v22a′=0−1,86222.(−2)=0,8668ms′=v′2−v22a′=0−1,86222.(−2)=0,8668m
f.
Thời gian chuyển động trên mặt phẳng ngang là:
t′=v′−va′=0−1,862−2=0,931s
Đáp án B.
Theo Ví dụ 1 Dạng 3, gia tốc của vật tự trượt xuống theo mặt phẳng nghiêng là a = gsin α - μ cos α
Do mặt phẳng nghiêng nhẵn μ = 0 ⇒ a = g sin α