Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Do x 1 v à x 2 vuông pha nên x 1 A 1 2 + x 2 A 2 2 = 1
Tương tự x 2 v à x 3 vuông pha nên: x 2 A 2 2 + x 3 A 3 2 = 1
Tại thời điểm t 2 : - 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
Tại thời điểm t 1
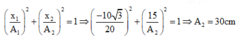
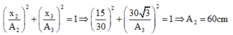
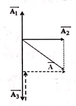
Từ giản đồ Frenel (hình vẽ) ta có: A = A 2 2 + ( A 3 - A 1 2 ) = 50 c m

Đáp án D
Ta nhận thấy x1 và x3 ngược pha nhau và cùng vuông pha với x2 nên khi x2 cực tiểu thì x1;x3 cực đại
![]()
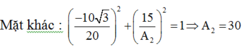
Biên độ dao động tổng hợp :
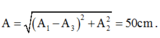

- Ta nhận thấy x1 và x3 ngược pha nhau và cùng vuông pha với x2 nên khi x2 cực tiểu thì x1; x3 cực đại:
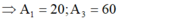
- Mặt khác:
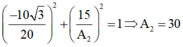
- Biên độ dao động tổng hợp:
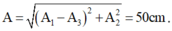


+ Do x1 và x2 vuông pha nên: x 1 A 1 2 + x 2 A 2 2 = 1
+ Tương tự x2 và x3 vuông pha: x 2 A 2 2 + x 3 A 3 2 = 1
+ Tại thời điểm t 2 : − 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
+ Tại thời điểm t 1 : x 1 A 1 2 + x 2 A 2 2 = 1 ⇒ − 10 3 20 2 + 15 A 2 2 = 1 ⇒ A 2 = 30 c m
x 2 A 2 2 + x 3 A 3 2 = 1 ⇒ 15 30 2 + 30 3 A 1 2 = 1 ⇒ A 3 = 60 c m
+ Từ giản đồ: A = A 2 2 + A 3 − A 1 2 = 50 c m
Chọn đáp án A

Chọn đáp án B
Nhận thấy x 1 và x 3 ngược pha nhau và cùng vuông pha với x 2 nen tại thời điểm t 2 thì x 2 = 0 nên
x 1 = − 20 c m = − A 1 ; x 3 = 60 c m = A 3
Mặt khác x 1 vuông pha x 2 nên tại thời điểm t 1 ta có:
− 10. 3 2 20 2 + 15 2 A 2 2 = 1 ⇒ A 2 = 30 .
Biên độ dao động tổng hợp:
A = A 1 − A 3 2 + A 2 2 = 40 2 + 30 2 = 50 c m

Hướng dẫn: Chọn đáp án B
Hai thời điểm t2 và t1 vuông pha nên biên độ tính theo công thức:
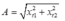
Với
![]()
![]()
![]()
Tổng hợp theo phương pháp cộng số phức:
![]()
![]()
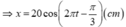
Chú ý: Nếu bài toán cho biết trạng thái của hai dao động thành phần ở cùng một thời điểm nào đó, yêu cầu tìm trạng thái của dao động tổng hợp thì có thể làm theo hai cách (vòng tròn lượng giác và giải phương trình lượng giác).




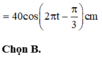
Đáp án B
Nhận thấy x1 và x3 ngược pha nhau và cùng vuông pha với x2 nên khi x2 (min) là x1, x3 (max) tại thời điểm t2 thì x 2 = 0 c m nên
Mặt khác x1 vuông pha x2 nên tại thời điểm t1 ta có:
Biên độ dao đổng tổng hợp: