Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
+ Thế năng của vật tại vị trí lò xo giãn cực đại:
![]()
Động năng khi đó: Wđ = 0.
Ngay sau khi tiến hành giữ chặt lò xo tại vị trí cách vật một đoạn l, lò xo còn lại dao động có chiều dài tự nhiên là: l’0
Coi lò xo giãn đều, nên ta có:
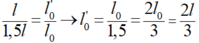
→ Độ cứng của lò xo mới là: k’ = 1,5k
+ Thế năng của vật ngay sau khi giữ:
![]()
Động năng của vật ngay sau khi giữ: W’đ = 0
Cơ năng của vật ngay sau khi giữ:
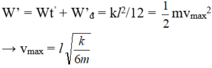

Nhớ biểu thức sau, rất hữu ích khi thi trắc nghiệm
\(W_d=n.W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{n+1}}\)
\(W_d=3W_t\Rightarrow x=\pm\dfrac{A}{\sqrt{3+1}}=\pm\dfrac{A}{2}\)
\(\Rightarrow F_{dh}=k.\Delta l=k.\dfrac{A}{2}=\dfrac{1}{2}kA\left(N\right)\)
\(F_{dh\left(max\right)}=kA\left(N\right)\)
\(\Rightarrow\dfrac{F_{dh}}{F_{dh\left(max\right)}}=\dfrac{\dfrac{1}{2}kA}{kA}=\dfrac{1}{2}\)

Độ biến dạng của lò xo tại vị trí cân bằng
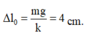
+ Chọn gốc tọa độ tại vị trí cân bằng, chiều dương hướng lên → lực đàn hồi bằng lực phục hồi
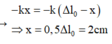
Đáp án D

Đáp án B
Tần số góc của dao động ω = k m = 100 0 , 2 = 10 5 rad/s → T = 0,281 s.
+ Độ biến dạng của lò xo tại vị trí cân bằng Δ l 0 = m g k = 0 , 1.10 100 = 2 cm
→ Kéo vật xuống vị trí lò xo giãn 6 cm rồi thả nhẹ → lò xo sẽ dao động với biên độ A = 6 – 2 = 4 cm.
+ Với E d = E d h ↔ E – E t = E d h → 1 2 k A 2 − 1 2 k x 2 = 1 2 k Δ l 0 + x 2 → 2 x 2 + 2 Δ l 0 x + Δ l 0 2 − A 2 = 0
Thay các giá trị đã biết vào phương trình, ta thu được x 2 + 2 x – 6 = 0 → hoặc x = 1,65 cm hoặc x = –3,65 cm.
→ Thời gian gần nhất kể từ thời điểm ban đầu (vật đang ở biên là) Δ t min = a r cos 1 , 65 4 360 0 0 , 281 = 51 , 3 m s

Giải thích: Đáp án A
Phương pháp: Công thức tính lực đàn hồi ![]()
Cách giải :
Trong quá trình dao động của vật lò xo bị nén ![]()
Ta có 
Vậy thời gian lò xo bị nén trong một chu kì là 
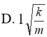
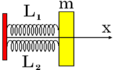


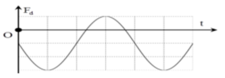
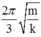
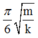
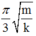
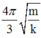
Chọn A
Thế năng đàn hồi của lò xo là: W t = 1 2 k ∆ l 2