Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(k=\omega^2.m=\left(10\sqrt{10}\right)^2.0,2=200\)
Tại thời điểm t, vận tốc của vật có độ lớn: \(v=\dfrac{p}{m}=\dfrac{0,1\sqrt{10}}{0,2}=0,5\sqrt{10}\left(\dfrac{m}{s}\right)=50\sqrt{10}\left(\dfrac{cm}{s}\right)\)
Tại tời điểm t + T/2 vật có li độ: \(x=\dfrac{10\sqrt{3}}{200}.100=5\sqrt{3}\left(cm\right)\)
Ta có: \(\omega=\dfrac{v_t}{x_{t+\dfrac{T}{2}}}=\dfrac{50\sqrt{10}}{5\sqrt{3}}\ne10\sqrt{10}\)
Sai ở đâu không nhỉ ?

+ Ta có
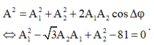
Để phương trình trên tồn tại nghiệm A 1 thì
![]()
Thay giá trị A 2 vào phương trình đầu, ta tìm được
![]()
Đáp an A

Đáp án A
Dựa vào pt đề bài cho, ta tìm được x 1 m ax = 1 , 5 ( c m ) x 2 m ax = 2 ( c m ) ⇒ A 1 = 1 , 5 ( c m ) A 2 = 2 ( c m )
Mặt khác, khi x1 max thì x 2 = 0 và ngược lại nên 2 dao động này vuông pha nhau. Dễ dàng tìm được biên độ dao động tổng hợp A = A 1 2 + A 2 2 = 2 , 5 ( c m )
Lực kéo về cực đại F k v m ax = k A = m ω 2 A = 0 , 75 ( N )

Hướng dẫn: Chọn đáp án B
Cách 1:
![]()
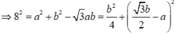
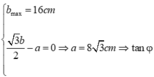
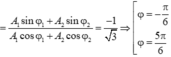
Cách 2: Áp dụng định lý hàm số sin ta có
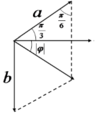
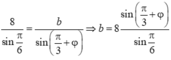
b đạt cực đại khi
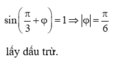



Chọn đáp án B
x = x 1 + x 2 = 5 ∠ π + 10 ∠ − π 3
= 5 3 ∠ − π 2
⇒ F max = k . A = ω 2 . m . A
= 10 2 .0 , 1.5 3 .10 − 2 = 0 , 5 3 N .
bn ơi cho mn hỏi s có 10^-2 v