Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(F=-k.x\)
\(\Rightarrow x = -\dfrac{F}{k}=-0,05\cos(2\pi t-\dfrac{5\pi}{6})(m)\)
Vận tốc: \(v=v'_{(t)}=0,1.\pi.\sin(2\pi t-\dfrac{5\pi}{6})\)(m/s)
Đến đây chưa xong nha
Bạn phải biến đổi tiếp từ x = -0,05.cos(2πt - \(\dfrac{5\pi}{6}\)) = 0,05.cos(2πt - \(\dfrac{\pi}{6}\))(m)
=> x = 5.cos(2πt - \(\dfrac{\pi}{6}\)) (cm)
=> v = 10π.sin(2πt - \(\dfrac{\pi}{6}\)) = 10π.cos(2πt + \(\dfrac{2\pi}{3}\)) < Đây mới là đáp án cuối cùng nha>

\(A=\dfrac{40\pi}{8\pi}=5\left(cm\right)\)
Vận tốc nhanh pha hơn li độ=> pha ban đầu của vật là: \(\varphi_d=\dfrac{5\pi}{6}-\dfrac{\pi}{2}=\dfrac{\pi}{3}\left(rad\right)\)
Góc quay được trong delta t là: \(\varphi=\omega\Delta t=8\pi.\dfrac{5}{24}=\dfrac{5}{3}\pi\left(rad\right)=\pi+\dfrac{2.\pi}{3}\left(rad\right)\)
Nghĩa là vật sẽ quay được một nửa đường tròn, rồi quay thêm 2 lần góc pi/3
Tức là đi được \(S=2A+\dfrac{A}{2}+A=\dfrac{7}{2}A=\dfrac{7}{2}.5=17,5\left(cm\right)\)
\(v_{tb}=\dfrac{s}{\Delta t}=\dfrac{17,5}{\dfrac{5}{24}}=84\left(cm/s\right)\)
Sao đề bài lại cho 74cm/s mà ko phải là 84cm/s nhỉ?
Cảm ơn bạn đã giúp, vì là đề thầy đưa nên mình cũng không rõ

Đáp án C
Phương pháp: Áp dụng hệ thức độc lập với thời gian của li độ và vận tốc
Cách giải:
Áp dụng hệ thức độc lập:
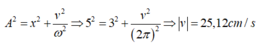

Chọn gốc thời gian lúc vật ở vị trí 2,5√2 (em ghi sai chổ đó)

Đáp án B
Vật đạt vận tốc cực đại khi qua vị trí cân bằng theo chiều dương. Trong một chu kỳ, vật đạt vận tốc cực đại 1 lần. → Trong t = 1 s = 1 T thì vật đạt vật tốc cực đại 1 lần.

Biểu diễn hai vecto A1 và A2 độ lớn lần lượt là √3/2 cm, √3 cm hợp với trục Ox lần lượt các góc 90o và 150o.
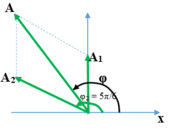
Ta có công thức :
A2 = A12 + A22 + 2A1A2 cos(φ2 - φ1) ⇒ A = 2,3 cm
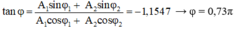
Vậy phương trình tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm)
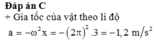
\(A^2=x^2+\dfrac{v^2}{\omega^2}\Rightarrow v=...\)