Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mỗi ô tô chở được:
120 : 3 = 40 (học sinh)
Số ô tô để chở học sinh đợ thứ hai là:
160 : 40 = 4 (ô tô)
Đáp số: 4 ô tô.

Số cách chọn 7 em bất kì trong ba khối: \(C|^7_{18}=31824\) (cách)
- Số cách chọn 7 em đi trong 1 khối:
\(C^7_7=1\) (cách)
- Số cách chọn 7 em đi trong 2 khối:
+) 7 em trong khối 12 và 11:
\(C^7_{13}-C^7_7=1715\) (cách)
+) 7 em trong khối 12 và 10:
\(C^7_{12}-C^7_7=791\) (cách)
+) 7 em trong khối 11 và 10:
\(C^7_{11}=330\) (cách)
→ Số cách chọn 7 em đi có cả ba khối:
31824 - 1 -1715 - 791 - 330 = 28987(cách)

n(omega)=\(C^7_{18}\)
\(n\left(\overline{A}\right)=C^7_{13}+C^7_{11}+C^7_{12}\)
=>\(P\left(A\right)=1-\dfrac{2838}{31824}=\dfrac{4831}{5304}\)

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
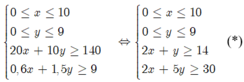
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

Q(x)=x^5(3x-5)^7
Số hạng chứa x^10 sẽ tương ứng với số hạng chứa x^5 trong (3x-5)^7
SHTQ là: \(C^k_7\cdot\left(3x\right)^{7-k}\cdot\left(-5\right)^k=C^k_7\cdot3^{7-k}\cdot\left(-5\right)^k\cdot x^{7-k}\)
Số hạng chứa x^5 tương ứng với 7-k=5
=>k=2
=>Số hạng cần tìm là: 127575x^10