Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Số cách chọn ngẫu nhiên 1 học sinh của tổ đó đi trực nhật là
C 11 1 = 11

Đáp án C.
Số cách chọn 5 học sinh trong đó có cả nam lẫn nữ là:
![]()

Đáp án: D.
![]()
Số cách chọn 3 học sinh có cả nam và nữ là
![]() .
.
Do đó xác suất để 3 học sinh được hcọn có cả nam và nữ là 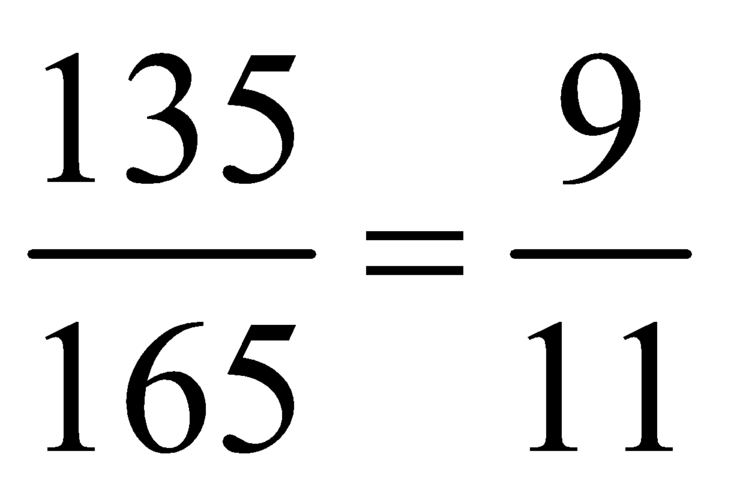 .
.

Đáp án C.
Phương pháp:
+) Chọn 2 học sinh nam.
+) Chọn 3 học sinh nữ.
+) Sử dụng quy tắc nhân.
Cách giải:
Số cách chọn 2 học sinh nam C 6 2
Số cách chọn 3 học sinh nữ C 9 3
Vậy số cách chọn 5 học sinh đi lao động trong đó có 2 học sinh nam là C 6 2 . C 9 3 .

Đáp án B
Chọn 2 nam từ 6 nam có C 6 2 cách
Chọn 4 nữ từ 9 nữ có C 9 4 cách
Do đó có C 6 2 . C 9 4 cách thỏa mãn

Đáp án B
chọn 6 học sinh đi lao động, trong đó 2 học sinh nam (và có 4 học sinh nữ) có C 6 2 . C 9 4 cách

Đáp án B
Phải chọn 2 học sinh nam và 4 học sinh nữ => Theo quy tắc nhân số cách chọn là C 6 2 . C 9 4 (cách).

Ta thực hiện các công đoạn sau:
Bước 1: Chọn 1 nam trong 7 nam làm tổ trưởng, có ![]() cách.
cách.
Bước 2: Chọn 1 nữ trong 6 nữ làm thủ quỹ, có ![]() cách.
cách.
Bước 3: Chọn 1 tổ phó trong 11 bạn còn lại (bỏ 2 bạn đã chọn ở bước 1 và bước 2), có ![]() cách.
cách.
Bước 4: Chọn 2 tổ viên trong 10 bạn còn lại (loại 3 bạn đã chọn ở trên), có ![]() cách.
cách.
Theo quy tắc nhân có ![]() cách chọn một tổ thỏa yêu cầu.
cách chọn một tổ thỏa yêu cầu.
Chọn A
Đáp án B.
Số cách chọn ngẫu nhiên một học sinh của tổ đó trực nhật là: 5+6=11 (cách).