Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
Ta có gốc thế năng tại tầng thứ 10 nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là: z =100 – 40 = 60m.
Thế năng của thang máy là: W t = m g z = 1000.9 , 8.60 = 588 k J
Đáp án: A

Lời giải
Ta có, gốc thế năng tại tầng thứ mặt đất nên khoảng cách từ thang máy khi ở tầng cao nhất đến gốc là:
z=60m+40m=100m
Thế năng của thang máy khi ở tầng cao nhất là:
W t = m g z = 1000 . 9 , 8 . 10 = 980000 J = 980 k J .
Đáp án: C

20/ \(A_P=P.s.\cos0=4000.10=40000\left(J\right)\)
21/ \(P=\frac{A}{t}=\frac{P.h}{t}=\frac{10^5.30}{1}=3.10^6\left(W\right)\)
22/ \(W_t=mgh=1000.9,8.\left(100-40\right)=588000\left(J\right)\)

a) Dễ chứng minh được: \(h_{max}=h+\dfrac{v_0^2}{2g}=4,8\left(m\right)\) ( bảo toàn hoặc dùng kiến thức ném thẳng đứng đều ra được )
b) Vật chỉ chịu tác dụng của trọng lực bảo toàn cơ năng: ( gốc thế năng tại mặt đất )
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz_1=2mgz_2\Rightarrow z_2=....\) ( tự tính )
tương tự bảo toàn cơ năng:
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz_1=\dfrac{1}{2}.2.mv_2^2\Rightarrow v_2=.....\) ( tự tính )
tham khảo link bài làm
https://hoidap247.com/cau-hoi/380596

a) Dễ chứng minh được: \(h_{max}=\dfrac{v_0^2}{2g}\) chọn gốc thế năm ở mặt đất nên: \(h_{max}=4+\dfrac{v_0^2}{2g}=4,8\left(m\right)\)
b) Bảo toàn cơ năng: \(W_1=W_2\Leftrightarrow m\left(\dfrac{1}{2}v_1^2+gz_1\right)=2mgz_2\Rightarrow z_2=.....\)
Hoàn toàn tương tự: \(W_1=W_2\Leftrightarrow m\left(\dfrac{1}{2}v_1^2+gz_1\right)=2.\dfrac{1}{2}mv_2^2\Rightarrow v_2=....\) Tính nốt :D

a)Thế năng tại mặt đất:
\(W=mgz=0J\)
b)Thế năng tại tầng hai:
\(W=mgz'=0,2\cdot10\cdot5\cdot2=20J\)
c)Thế năng tại tầng 5:
\(W=mgz''=0,2\cdot10\cdot5\cdot5=50J\)

a, Ngoại lực tác dụng lên thang máy là trọng lực và kéo của động cơ thang máy. Áp dụng định lý về động năng ta có: Wđ1 – Wđ0 = A F 1 → + A P 1 →
Mà Wđ1 = m . v 1 2 2 , Wđ0 = m . v 0 2 2 = 0 ;
A P 1 → = − P . s 1 = − m . g . s 1 ( A P → 1 < 0 )
Vì thang máy đi lên
⇒ A F 1 = m . v 1 2 2 + m . g . s 1 = 1 2 .1000.5 2 + 1000.10.5 = 62500 J
b, Vì thang máy chuyển động đều, lực kéo của động cơ cân bằng với trọng lực P → : F 2 → + P → = 0 . Công phát động của động cơ có độ lớn bằng công cản A F 2 → = − A P → với A P = − P . s 2 = − m . g . s 2
=> AF2 = mgs2 do đó công suất của động cơ thang máy trên đoạn đường s2 là:
℘ 2 = A F 2 t = m . g . s 2 t = m . g . v 2 = m . g . v 1 ⇒ ℘ 2 = 1000.10.5 = 50000 ( W ) = 50 ( k W ) .
c, Ngoại lực tác dụng lên thang máy là trọng lực P → và lực kéo F 3 → của động cơ.
Áp dụng định lí động năng ta có: Wđ3 – Wđ2 = AF3 + Ap’
Mà Wđ3 = m . v 3 2 2 = 0 ; Wđ2 = m v 2 2 2 (v2 = v1 = 5m/s); Ap = - Ps3 = - mgs3
Công của động cơ trên đoạn đường s3 là: AF3 = mgs3 - m v 2 2 2 = 37500J
Áp dụng công thức tính công ta tìm được lực trung bình do động cơ tác dụng lên thang máy trên đoạn đường s3: F 3 ¯ = A F 3 s 3 = 37500 5 = 7500 N

Đáp án C
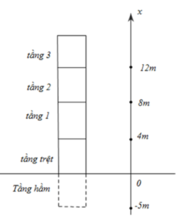
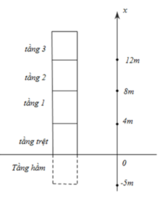
Từ hình vẽ, ta có:
Độ dời khi từ hầm lên đến tầng 3:
s 3 = x T − x H = 12 − ( − 5 ) = 17 ( m )

Đáp án A
Ta có: Thang máy di chuyển từ tầng trệt - tầng hầm - tầng trệt - tầng 1 - tầng 2 - tầng 3:

=> Quãng đường chuyển động khi người này lên đến tầng 3 là:
S=5.2+4+4+4=22m
Chọn gốc thế năng tại điểm cách mặt đất 40m
Độ cao cao nhất đến gốc là: z =100 – 40 = 60m
thế năng của thang máy ở tầng cao nhất là
`W=mgz=1000*9,8*60=588000J`