Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn đáp án C
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng → A B = 4 λ . Chuẩn hóa λ = 1 .
Ta có:
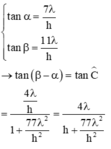
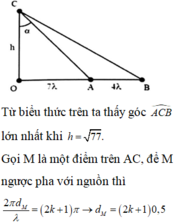
Từ biểu thức trên ta thấy góc A C B ^ lớn nhất khi h = 77 .
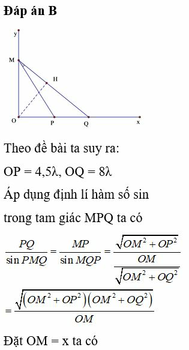
Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
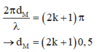
Với khoảng giá trị tính về phía C từ đường vuông góc của O lên AC:
kết hợp với chức năng Mode → 7 ta tìm được 4 vị trí.
Tương tự như vậy, ta xét đoạn về phía A: 
ta tìm được 2 vị trí
→ Trên AC có 6 vị trí.
Đáp án C
Giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng
Chuẩn hóa λ = 1
Ta có:
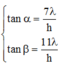
= tan ∠ C
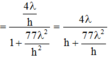
→ Từ biểu thức trên, ta thấy rằng góc ∠ A C B lớn nhất khi
Gọi M là một điểm trên AC, để M ngược pha với nguồn thì
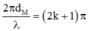
Với khoảng giá trị của d M , tính về phía C từ đường vuông góc của O lên AC:
kết hợp với chức năng Mode → 7 ta tìm được 4 vị trí
Tương tự như vậy ta xét đoạn về phía A: 
ta cũng tìm được 2 vị trí.
→ Trên AC có 6 vị trí
Bình luận: Thay vì đạo hàm hay dùng bất đẳng thứcCô Si thì các em học sinh có thể dùng máy tính cầm tay để tìm giá trị nhỏ nhất rất nhanh chóng.
v Như vậy với cách làm này thì các em cũng có thể tìm được giá trị của để cho diện tích tam giác MCD nhỏ nhất.
Đáp án C
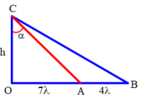
Để đơn giản, ta chọn λ = 1 → A B = 6 , 6
Để một điểm trên A C cực đại và cùng pha với nguồn thì d 1 + d 2 = k d 1 + d 2 = n ≥ A B = 6 , 6 . Trong đó n và k có độ lớn cùng chẵn hoặc lẻ
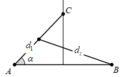
Mặc khác để khoảng cách A C là ngắn nhất thì cos α = A B 2 + d 1 2 − d 2 2 2 A B . d 1 phải lớn nhất
Ta để ý rằng khi xảy ra cực đại thì mỗi bên trung trực của A B có 6 dãy cực đại ứng với k = 1 , ± 2..... ± 6 . Với mỗi giá trị của k ta tìm được cặp giá trị d 1 , d 2
→ Thử các giá trị của k , nhận thấy cos α lớn nhất khi k = 1 và d 1 = 3 d 2 = 4
→ h min = A B 2 tan α ≈ 1 , 3757
Đáp án B
Bước sóng của sóng 
Để điểm M là một điểm nằm giữa BC cùng pha với A thì
+ Với khoảng giá trị của 
, kết hợp với chức năng Shift → Solve của casio ta tìm được 5 vị trí cùng pha
