
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

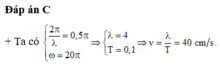

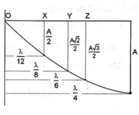
Đáp án B
Biên độ tại bụng sóng: A= 2mm
Tại điểm có biên độ 2 mm
Khoảng cách từ Y đến bụng sóng
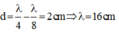
Tại điểm cách nút 4cm:
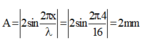 (bụng sóng)
(bụng sóng)
Vận tốc dao động của điểm trên dây cách nút 4cm
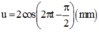
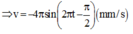
Tại thời điểm 1s: 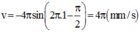

\(u = 40 \sin (2,5\pi x)\cos (\omega t) ;(m,s)\)
So sánh với phương trình tổng quát: \(u = a \sin (\frac{ 2\pi x}{\lambda}+ \varphi)\cos (\omega t+\varphi_1 ) ;(m,s)\)
=> \(2,5\pi = 2\pi\frac{x}{\lambda}\)
=> \(\lambda = 0,8m.\)
Biên độ của điểm N cách một nút sóng 10 cm = 0,1 m là \(a_N = 40 \sin (2,5.\pi.0,1) = \frac{40}{\sqrt{2}}.\)
khoảng thời gian ngắn nhất giữa 2 lần liên tiếp để một điểm trên bụng có độ lớn li độ bằng biên độ của điểm N là
=> Góc quay được kí hiệu màu đỏ.
\(t = \frac{\varphi}{\omega} = \frac{2.\pi/4}{2\pi T} = \frac{T}{4}s. \)
mà \(t = 0,125s=> T = 0,5s.\)
=> \(v = \frac{\lambda}{T} = \frac{0,8}{0,5}=1,6m/s=160cm/s.\)
Chọn đáp án.B.160cm/s.

Đáp án B
Ta có : λ = v f = 12 cm ⇒ MN = 37 cm = 3 λ + λ 12
Vì sóng tuần hoàn theo không gian nên sau điểm M đoạn 3λ có điểm M’ có tính chất như điểm M nên ở thời điểm t điểm M’ cũng có li độ uM’= -2 mm và đang đi về VTCB.
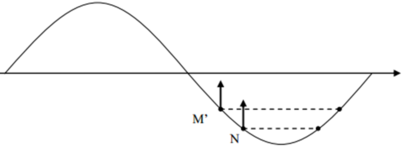
Vì uM’ = –2mm = –A/2 => xM’ = λ/12
Vì N cách M’ đoạn λ/12 => xN = λ/6.
Ta có : ∆ t = 89 80 s = 22 T + T 4 ⇒ lùi về quá khứ T 4
=> điểm N có li độ xN = –A/2
v N = - ωA 3 2 = - 80 π 3 ( mm / s ) .

chọn đáp án B
Từ phương trình 2.5
π
x
=
2
π
x
λ
=> landa=0.8m
Do thời gian liên tiếp để điểm trên bụng đến nút là
t
=
T
4
=
0
,
125
(vẽ hình ra sẽ thấy) =>T=0,5s => v=
λ
T
=160 m/s