Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
+ Độ lệch pha giữa hai điểm cách nhau một đoạn d trên cùng một phương truyền sóng
∆ φ = 2 πd λ

Phương trình sóng tổng hợp tai điểm N như sau:
\(u_N = 2A \cos \pi (\frac{\Delta \varphi}{2\pi}-\frac{d_2-d_1}{\lambda}).\cos (\omega t + \frac{\varphi_1+\varphi_2}{2\pi}-\frac{d_1+d_2}{2\lambda})\)
với \(A_N= |2A \cos \pi (\frac{\Delta \varphi}{2\pi}-\frac{d_2-d_1}{\lambda})|\)
Theo bài: \(d_2-d_1 = k\lambda; \Delta \varphi = \varphi_2-\varphi_1 = \pi.\)
=> \(A_N= |2A \cos \frac{\pi}{2}| = 0.\)
Như vậy đáp án Chọn đáp án.A

+ Phần tử sóng tại O dao động sớm pha hơn phần tử sóng tại M. Phương trình sóng tại O là:
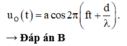

Ta có: \(v_{max}=\omega.A=\dfrac{2\pi}{T}.A=\dfrac{2\pi.v}{v.T}.A=\dfrac{2\pi.v}{\lambda}.A\)
Theo giả thiết: \(v_{max}=v\)
\(\Rightarrow \dfrac{2\pi.v}{\lambda}.A=v\)
\(\Rightarrow \lambda = 2\pi.A\)

+ Điểm O gần nguồn sóng hơn, do đó sẽ dao động sớm pha so với phần tử môi trường tại :
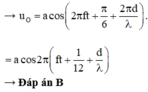
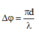
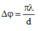
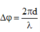


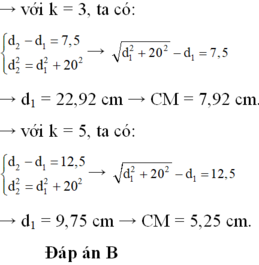
Đáp án D
+ Độ lệch pha giữa hai điểm M và N là ∆ φ = 2 π d λ