Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Thí sinh thi được 26 điểm do đó có 6 phương án đúng và 4 phương án sai
Xác suất cần tìm sẽ là:
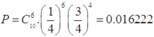
=> Chọn phương án A.
Chú ý: Công thức tổng quát cho bài toán n câu hỏi và a đáp án đúng sẽ là
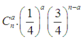
Đáp án B
Giả sử để đạt được 26 điểm thì số câu chọn đúng là a, sai là 10-a.
Ta có: 5a-1(10-a) = 26 => 6a = 36 => a = 6.
Vậy phải chọn được 6 câu đúng và 4 câu sai.
Xác suất chọn 1 câu được đúng là:
Xác suất chọn 1 câu được sai là:
Có 
cách chọn 6 câu đúng, 4 câu sai.
Vậy xác suất để được 26 điểm là:
Đáp án B
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25
Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25
Chọn A
Cách 1: Vì mỗi câu hỏi có bốn phương án trả lời và chỉ có một phương án đúng nên xác suất để trả lời đúng và xác suất để trả lời sai một câu hỏi lần lượt là 1 4 v à 3 4
Theo yêu cầu của bài toán có các trường hợp sau:
| Trường hợp |
Số câu trả lời đúng |
Số câu trả lời sai |
Xác suất xảy ra |
| TH1 |
8 |
2 |
(quy tắc nhân) |
| TH2 |
9 |
1 |
(quy tắc nhân) |
| TH3 |
10 |
0 |
(quy tắc nhân) |
Vậy áp dụng quy tắc cộng ta có xác suất cần tìm là:
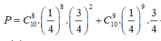
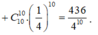
Cách 2:
- Số cách làm bài của thí sinh: 4 10 (cách).
- Để thí sinh đó đạt từ 8,0 điểm trở lên, ta có 3 trường hợp sau:
+ Làm được 8 câu đúng và 2 câu sai (8 điểm): 
+ Làm được 9 câu đúng và 1 câu sai (9 điểm): 
+ Làm được 10 câu đúng (10 điểm): 1 (cách).
Do đó số cách để thí sinh đạt từ 8,0 điểm trở lên là: 
Vậy xác suất cần tìm là 
Đáp án A
Với mỗi câu hỏi, thí sinh có 4 phương án lựa chọn nên số phần tử của không gian mẫu là
n Ω = 4 10
Gọi X là biến cố “thí sinh đó đạt từ 8,0 điểm trở lên”
TH1. Thí sinh đó làm được 8 câu ( tức là 8,0 điểm):
Chọn 8 câu trong số 10 câu hỏi và 2 câu còn lại mỗi câu có 3 cách lựa chọn
đáp án sai nên có C 10 8 . 3 2 cách để thí sinh đúng 8 câu
TH2. Thí sinh đó làm được 9 câu (tức là 9,0 điểm)
Chọn 9 câu trong số 10 câu hỏi
và câu còn lại có 3 cách lựa chọn đáp án sai
nên có C 10 9 . 3 1 cách để thí sinh đúng 9 câu
TH3. Thí sinh đó làm được 10 câu (tức là 10,0 điểm)
Chỉ có 1 cách duy nhất.
Suy ra số kết quả thuận lợi cho biến cố X là
Vậy xác suất cần tìm là
P = n ( X ) n ( Ω ) = 436 4 10
Đáp án A
Với mỗi câu hỏi, thí sinh có 4 phương án lựa chọn nên số phần tử của không gian mẫu là 
Gọi X là biến cố “thí sinh đó đạt từ 8,0 điểm trở lên”
TH1. Thí sinh đó làm được 8 câu (tức là 8,0 điểm): Chọn 8 câu trong số 10 câu hỏi và 2 câu còn lại mỗi câu có 3 cách chọn đáp án sai nên có 
cách để thí sinh đúng 8 câu.
TH2. Thí sinh đó làm được 9 câu (tức là 9,0 điểm): Chọn 9 câu trong số 10 câu hỏi và câu còn lại có 3 cách lựa chọn đáp án sai nên có 
cách để thí sinh đúng 9 câu.
TH3. Thí sinh đó làm được 10 câu (tức là 10,0 điểm): Chỉ có 1 cách duy nhất .
Suy ra số kết quả thuận lợi cho biến cố X là
Vậy xác suất cần tìm là
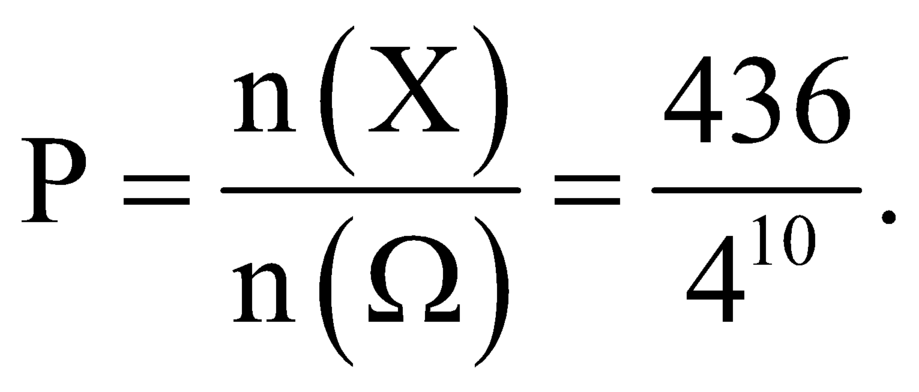
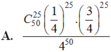
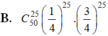
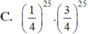
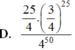
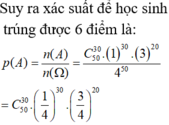
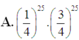
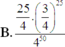
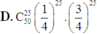
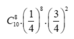
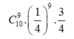
Đáp án A
Với 10 câu trắc nghiệm sẽ có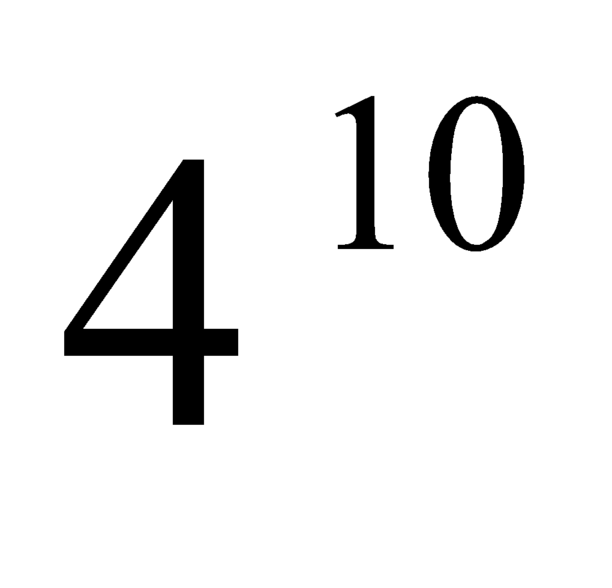
cách chọn đáp án.
Và bài điền tiếp theo chắc chắn sẽ giống 1 trong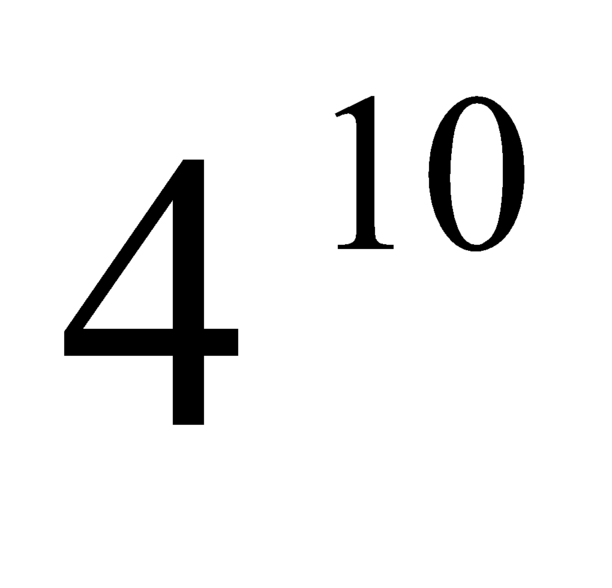
bài điền trước đó.
Vậy có tất cả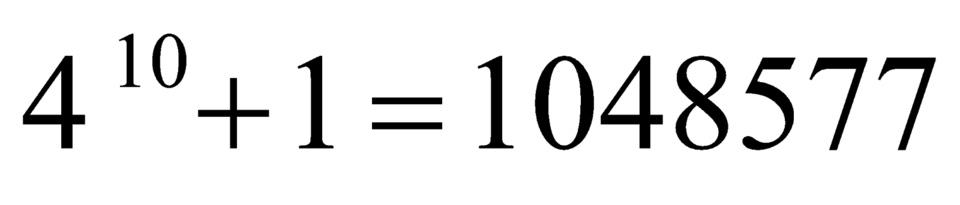
phiếu thỏa mãn yêu cầu bài toán.