Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng vân: \(i=\dfrac{\lambda D}{a}=\dfrac{0,5\cdot10^{-6}\cdot1}{0,5\cdot10^{-3}}=1\cdot10^{-3}m=1mm\)
Tại M trên màn E cách vân trung tâm một khoảng x=3,5mm nên:
\(\Rightarrow x=3,5=k\cdot i=k\cdot1\)
\(\Rightarrow k=3,5\Rightarrow\)Vân tối thứ 4.
Chọn D.

Đáp án D
Khoảng vân 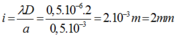
*Khoảng cách giữa một vân sáng và một vân tối cạnh nhau được tính bởi
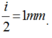 .
.

Phương pháp
Áp dụng công thức tính khoảng vân trong giao thoa sóng ánh sáng
Cách giải:
ta có khoảng vân i = λ D a
khoảng cách giữa một vân sáng và một vân tối trong giao thoa sóng ánh sáng sáng là một nửa khoảng vân = 1mm
=> Chọn D

Chọn B
Ta có: 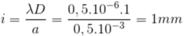
Tại điểm M ta có:
x = 3,5mm = 3,5i => Vân tối thứ 4

Màu sắc của vân trung tâm được tạo thành do sự chồng chập của ba ánh sáng đơn sắc λ 1 , λ 2 , λ 3
Vậy toạ độ những vân sáng cùng màu vân trung tâm thoả mãn
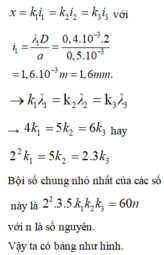

Vậy ta thấy giá trị khả dĩ lớn nhất của n bằng 4.
Vậy tổng số vân cùng màu vân trung tâm là N = 1 + 2.4 = 9 vân.
Đáp án C

\(i = \frac{\lambda D}{a} = \frac{0,5.1}{0,5} = 1 mm.\)
Số vân sáng trên trường giao thoa L là \(N_S =2 |\frac{L}{2i}|+1 = 2.|\frac{13}{2.1}|+1 = 2.6+1=13\)
Số vân tối trên trường giao thoa L là \(N_t =2 |\frac{L}{2i}+0,5| = 2.|\frac{13}{2.1}+0,5| = 2.7=14.\)
Chú ý: \(|\frac{L}{2i}|\) gọi là lấy phần nguyên của số \(\frac{L}{2i}\).
Ví dụ \(\frac{L}{2i} = 6,5 => |\frac{L}{2i}| = 6.\)
Chọn đáp án.A.

Đáp án B
+ Khoảng vân giao thoa của các ánh sáng đơn sắc

+ Ta xét các tỉ số:
x M i 1 = 3 , 3 x M i 1 = 13 , 3 → trên đoạn MN có các vị trí cho vân sáng từ bậc 4 đến bậc 13 của bức xạ λ1
x M i 2 = 2 , 56 x M i 2 = 10 , 25 → trên đoạn MN có các vị trí cho vân sáng từ bậc 3 đến bậc 10 của bức xạ λ2
+ Điều kiện trùng nhau của hai hệ vân
λ 1 λ 2 = k 2 k 1 = 10 13 → trên đoạn MN có một vị trí trùng nhau của hệ hai vân sáng, do đó số vân sáng quan sát được là
n
=
10
+
8
-
1
=
17
(ta trừ một là do hai vân sáng trùng nhau ta tính là một vân sáng)

Đáp án C
Khoảng vân: 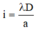
Vị trí của vân sáng bậc 2:
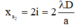
Vị trí của vân tối thứ 3:
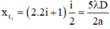
Khoảng cách từ vân sáng bậc 2 đến vân tối thứ 3 nằm về hai phía của vân trung tâm là:
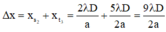

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)
D