Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Phương pháp:
Công thức lãi kép, không kỳ hạn: A n = M 1 + r % n
Với: A n là số tiền nhận được sau tháng thứ n,
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%)
Cách giải:
Thời gian người đó gửi: 15/4/2018 đến 15/3/2020 tương ứng với 23 tháng.
Ta có: A n = M 1 + r % n ⇔ 50 000 000 = M 1 + 0 , 55 % 23 ⇒ M ≈ 44 704 000 (đồng)

Áp dụng công thức lãi kép ![]() với A số tiền gửi vào lần đầu tiên, r = 0,55% là lãi suất mỗi tháng, n = 23 tháng và Tn = 50.000.000 đồng. Ta được
với A số tiền gửi vào lần đầu tiên, r = 0,55% là lãi suất mỗi tháng, n = 23 tháng và Tn = 50.000.000 đồng. Ta được
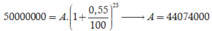 đồng. Chọn D.
đồng. Chọn D.

Gửi lần đầu thu về tổng số tiền 100 1 + 0 , 02 4 gửi lần kế tiếp thu về 100 1 + 0 , 02 2
Tổng số tiền nhận được sau đúng 1 năm kể từ lần gửi đầu tiên là
100 1 + 0 , 02 4 + 100 1 + 0 , 02 2 ≈ 212 . 283 . 000
đồng.
Chọn đáp án A.

Đáp án là A
Số tiền người đó có được sau đúng 6 tháng gửi là:
T 1 = 10 8 . 1 + 2 % 2 = 104.040.000 (đồng).
Số tiền người đó có được sau 1 năm khi người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó là:
T 2 = 104.000.000 + 100.000.000 1 + 2 % 2 = 212.283.216 (đồng).

Đáp án C
Gọi n là số năm cần gửi, suy ra 100 1 + 7 % n ≥ 250 ⇔ n ≥ 13,54 ⇒ n = 14

Đáp án A
Công thức lãi kép P n = P o ( 1 + r ) n = 100 ( 1 + 0 , 4 % ) 6 ≈ 102424000


