Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(i_1=3,5/7=0,5mm\)
\(i_2=7,2/8=0,9mm\)
Vân sáng: \(i=\dfrac{\lambda D}{a}\)
Suy ra: \(\dfrac{i_1}{i_2}=\dfrac{\lambda_1}{\lambda_2}\Rightarrow \lambda_2=\lambda_1.\dfrac{i_2}{i_1}=420.\dfrac{0,9}{0,5}=756nm\)

Khoảng vân là i = 3,6/(9 - 1) = 4,5mm
Từ công thức i = λ D/a suy ra
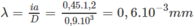

Chọn D.
Với bức xạ λ vị trí vân sáng bậc k = 3, ta có x k = k λD a . Với bức xạ λ' vị trí vân sáng bậc k', ta có x k ' = k ' λ ' D a . Hai vân sáng này trùng nhau ta suy ra xk = xk’ tương đương với kλ = k’λ’ tính được λ’ = 0,6μm

Khi quan sát vân bằng kính lúp thì ta trông thấy ảnh của hệ vân nằm trên mặt phẳng tiêu vật của kính lúp và ảnh đó ở xa vô cùng (H.25.1G).
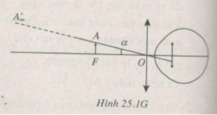
Ta thấy α = tan α = i/f = 12,5'
Khoảng cách từ hai khe tới mặt phẳng của các vân : D = L - f = 40 - 4 = 36 cm = 0,36 m.
Bước sóng của bức xạ là :
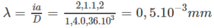

Chọn C
M cách vân trung tâm 1,2 mm người ta quan sát được vân sáng bậc 4 tức là:
xM = 4i và 4i = 1,2 mm => i = 0,03 mm
di chuyển từ từ màn quan sát ra xa và dọc theo dường thẳng vuông góc với mặt phẳng chứ hai khe thì thấy tại M chuyển thành vân sáng bậc ba tức là:
xM = 3i'
=> 3i' = 4i => i' = 0,4 mm
=> Δi = i' - i = 0,1 mm
Khi dời màn ra xa thêm 0,25 m thì khoảng vân tăng thêm 0,1 mm tức là:
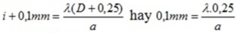
=> λ = 0,40 μm
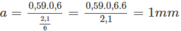
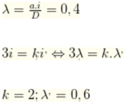
Với λ 0 , ta có i 0 = 3,3/(8 - 1) = 3,3/7 mm
Với λ ta có i = 3,37/(9 - 1) = 3,37/8 mm
Do đó ta có