Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi độ dài quãng đường AB là x
Thời gian đi là x/9(h)
Thời gian về là x/12(h)
Theo đề, ta có phương trình:
x/9-x/12=1/2
hay x=18
Gọi x(km) là quãng đường AB (x>0)
Thời gian đi từ A->B là :x/15 (h)
Thời gian đi từ B-> A là: x/12 (h)
Đổi 30 ph= 1/2 (h)
Ta có phương trình:
x/12 - x/15 = 1/2
<=> 5x- 4x=30
<=> x=30
Vậy quãng đường AB dài 30 km
Gọi thời gian đi là x (h) ( x>o)
Thời gian về là x+34(h)
Quãng đường đi 15x 3/4 (km)
Quãng đường về 12(x+3/4)(km)
Vì quãng đường AB lúc đi và về không đổi ---> phương trình
15x=12(x+34)
---> x=3(tmđk)
--->quãng đường AB dài :15.3=45(km)
Gọi x là quãng đường AB(x>0, km)
Ta có vận tốc lúc về là: 40+5=45(km/h)
Đổi 15'=1/4 h
Vì lúc về ít hơn lúc đi là 1/4 h, ta có pt:
\(\dfrac{x}{14}-\dfrac{1}{4}=\dfrac{x}{45}\)
\(\dfrac{9x}{360}-\dfrac{90}{360}=\dfrac{8x}{360}\)
\(9x-8x=90\)
\(x=90\)
Vậy: Độ dài quãng đường AB là 90km
Gọi q/đ `AB` là: `x (km)` `ĐK: x > 0`
`@` Thời gian đi là: `x/15 (h)`
`@` Thời gian về là: `x/12 (h)`
Vì t/gian về lâu hơn t/gian đi là `25 phút=5/12 h` nên ta có ptr:
`x/12-x/15=5/12`
`<=>[5x]/60-[4x]/50=25/50`
`<=>5x-4x=25`
`<=>x=25`(t/m)
Vậy q/đ `AB` dài `25 km`
Gọi x ( km ) là độ dài quãnh đường AB ( x > 0 )
Thời gian người đó đi từ A đến B là: \(\dfrac{x}{15}\) ( giờ )
Thời gian người đó đi về là: \(\dfrac{x}{12}\) ( giờ )
Vì thời gian về lâu hơn thời gian đi 25 ( = \(\dfrac{5}{12}\) giờ ) nên ta có phương trình:
\(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{5}{12}\)
\(\Leftrightarrow\dfrac{5x}{60}-\dfrac{4x}{60}=\dfrac{25}{60}\)
\(\Leftrightarrow5x-4x=25\)
\(\Leftrightarrow x=25\) ( nhận )
Vậy quãng đường AB dài 25 km
Gọi x(km) là độ dài quãng đường AB(Điều kiện: x>0)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{40}\left(h\right)\)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{45}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{40}-\dfrac{x}{45}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{9x}{360}-\dfrac{8x}{360}=\dfrac{90}{360}\)
\(\Leftrightarrow9x-8x=90\)
hay x=90(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 90km
Gọi x là quãng đường AB(x>0, km)
Ta có vận tốc lúc về là: 40+5=45(km/h)
Đổi 15'=1/4 h
Vì lúc về ít hơn lúc đi là 1/4 h, ta có pt:
\(\dfrac{x}{40}-\dfrac{1}{4}=\dfrac{x}{45}\)
\(\dfrac{9x}{360}-\dfrac{90}{360}=\dfrac{8x}{360}\)
\(9x-8x=90\)
\(x=90\)(tmđk)
Vậy sAB là: 90km
Gọi quãng đường $AB$ là $x(km;x>0)$
Thời gian đi từ $A$ đến $B$ là $\dfrac{x}{15}(h)$
Lúc về người đó đi với số thời gian là $\dfrac{x}{12}(h)$
do thời gian về lâu hơn thời gian đi là $45p=\dfrac{3}{4}(h)$
Nên ta có phương trình: $\dfrac{x}{15}+\dfrac{3}{4}=\dfrac{x}{12}$
$⇔\dfrac{3x}{180}=\dfrac{3}{4}$
$⇔x=\dfrac{3}{4}.180:3=45$
Vậy quãng đương $AB$ dài $45$ km
Gọi độ dài quãng đường AB là x
Thời gian đi là x/12
Thời gian về là x/18
Theo đề, ta có: x/12-x/18=3/4
hay x=27
Đổi 30 phút =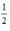
giờ.
Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0). Thời gian xe đi từ A đến B là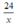
(giờ).
Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là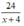
(giờ)
Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:
Giải phương trình:
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.
Chọn đáp án A