Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a,vận tốc trung bình trên cả quãng đường là
vtb=\(\dfrac{s1+s2+s3+...sn}{t1+t2+t3+...tn}\)

a) Vận tốc trung bình của người đó trên quãng đường s là:
\(v_{tb}=\dfrac{s}{t}=\dfrac{s_1+s_2+s_3+.....+s_n}{t_1+t_2+t_3+.....+t_n}\)
b) không biết làm!!!

Đáp án B
Vật tốc trung bình của người đi xe đạp đó là: v = s 1 + s 2 + s 3 t 1 + t 2 + t 3

Đáp án B
Vật tốc trung bình của người đi xe đạp đó là: v = s 1 + s 2 + s 3 t 1 + t 2 + t 3

Chọn C
Công thức tính vận tốc trung bình của người này trên hai quãng đường s1 và s2 là:
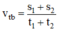

\(2\)m/s=7,2km/s
Thời gian người đó đi quãng đường thứ nhất : \(t=\dfrac{s}{v}=\dfrac{3}{7,2}=\dfrac{4}{5}\left(h\right)\)
Vận tóc TB của 2 quãng đường : \(v_{tb}=\dfrac{s+s'}{t+t'}=\dfrac{3+1,95}{\dfrac{4}{5}+0,5}\approx3,53\)(km/h)
đổi 3 km = 0,003 m
Thời gian người đi bộ đầu tiên là
\(t=\dfrac{s}{v}=0,003:2=0,0015\left(s\right)\)
đổi 0,0015 s = 0,0000004 h
Vận tốc trung bình của người đó trên cả 2 quãng đường là
\(V_{tb}=\dfrac{S+S_1}{t+t_1}=\dfrac{3+1,95}{0,5+0,0000004}=\dfrac{4,95}{0,5000004}=9,8\left(kmh\right)\)

Vận tốc trung bình:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{300+900}{\dfrac{300}{1,5}+5\cdot60}=2,4\)m/s

Vận tốc trung bình của người đó trên quãng đường S là :
\(v_{tb}=\dfrac{s_1+s_2+s_3+...+s_n}{t_1+t_2+t_3+...+t_n}\)
Ta có : \(v_{tb}=\dfrac{v_1.t_1+v_2t_2+v_3t_3+...+v_nt_n}{t_1+t_2+t_3+...+t_n}=v_{min}.\dfrac{\dfrac{v_1}{v_{min}}.t_1+\dfrac{v_2}{v_{min}}.t_2+\dfrac{v_3}{v_{min}}.t_3+...+\dfrac{v_n}{v_{min}}.t_n}{t_1+t_2+t_3+...+t_n}\)
Do : \(\dfrac{v_1}{v_{min}};\dfrac{v_1}{v_{min}}...\dfrac{v_1}{v_{min}}>1nên\dfrac{v_1}{v_{min}}.t_1+\dfrac{v_1}{v_{min}}.t_2+\dfrac{v_1}{v_{min}}.t_3+...+\dfrac{v_1}{v_{min}}.t_n>t_1+t_2+t_3+...+t_n\)
=> vmin < vtb
Ta có :
\(v_{tb}=\dfrac{v_1t_1+v_2t_2+...+v_nt_n}{t_1+t_2+t_3+...+t_n}=v_{max}.\dfrac{\dfrac{v_1}{v_{max}}.t_1+\dfrac{v_2}{v_{max}}.t_2+...+\dfrac{v_n}{v_{max}}.t_n}{t_1+t_2+t_3+...+t_n}\)
Do : \(\dfrac{v_1}{v_{max}};\dfrac{v_1}{v_{max}}...\dfrac{v_1}{v_{max}}< 1\)
Nên : \(\dfrac{v_1}{v_{max}}.t_1+\dfrac{v_1}{v_{max}}t_2+\dfrac{v_1}{v_{max}}t_3+...+\dfrac{v_n}{v_{max}}.t_n< t_1+t_2+...t_n\)
=> vmax > vtb
Nguon : https://www.slideshare.net/Harvardedu/cc-bi-ton-v-vn-tc-trung-bnh-ca-vt-chuyn-ng