Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
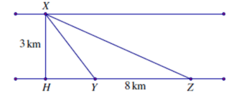
Đặt H Y = x 0 ≤ x ≤ 8 khi đó thời gian người đó đến Z là: f x = 1 6 9 + x 2 + 1 8 8 − x
f ' = x 6 9 + x 2 − 1 8 = 4 x − 3 9 + x 2 24 9 + x 2 ⇒ f ' = 0 ⇔ x = 9 7
⇒ M i n f = M i n f 0 ; f 8 ; f 9 7 = M i n 3 2 ; 73 6 ; 7 8 + 1 = 1 + 7 8

Đáp án B
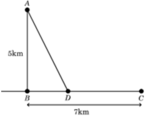
Gọi A D = x 5 ≤ x ≤ 74 . Khi đó thì B D = x 2 − 25 ⇒ C D = 7 − x 2 − 25 .
Tổng thời gian đi từ A đến C là

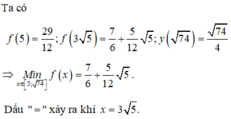

Đáp án B
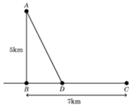
Gọi A D = x 5 ≤ x ≤ 74 . Khi đó thì B D = x 2 − 25 ⇒ C D = 7 − x 2 − 25 .
Tổng thời gian đi từ A đến C là f x = A D 4 + C D 6 = x 4 + 7 − x 2 − 25 6 . Ta cần tìm giá trị nhỏ nhất của hàm f x này trên 5 ; 74 .
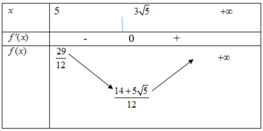
Có f ' x = 1 4 − x 6 x 2 − 25 ; f ' x = 0 ⇔ 3 x 2 − 25 = 2 x ⇔ x ≥ 0 9 x 2 − 25 = 4 x 2 ⇔ x ≥ 0 x = 3 5 x = − 3 5 ⇔ x = 3 5 .
Ta có f 5 = 29 12 ; f 3 5 = 7 6 + 5 12 5 ; y 74 = 74 4
⇒ M i n x ∈ 5 ; 74 f x = 7 6 + 5 12 5 . Dấu " = " xảy ra khi x = 3 5 .

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
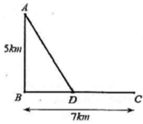
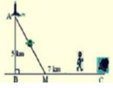
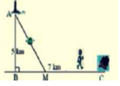
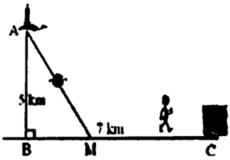
Đặt BM= x , CM =7-x-> A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
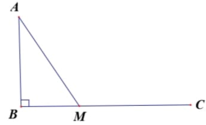
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án B
Trước tiên ta xác định hàm số f(x) là hàm số tính thời gian người canh hải đăng phải đi.
Đặt BM= x , CM =7-x ⇒ A M = x 2 + 25 . Theo đề ta có ngưới canh hải đăng chèo từ A đến M trên bờ biển với v = 4km/h rồi đi bộ đến C với v = 6 km/h
⇒ f ( x ) = x 2 + 25 4 + 7 − x 6 = 3 x 2 + 25 − 2 x + 14 12 với x ∈ ( 0 ; 7 )
f ' ( x ) = 1 12 3 x x 2 + 25 − 2 f ' ( x ) = 0 ⇔ 3 x x 2 + 25 − 2 = 0 ⇔ 3 x − 2 x 2 + 25 = 0 ⇔ 2 x 2 + 25 = 3 x ⇔ 5 x 2 = 100 x ≥ 0 ⇔ x = ± 2 5 x ≥ 0 ⇔ x = 2 5
Vậy đoạn đường ngắn nhất thì giá trị phải nhỏ nhất
f ( 0 ) = 29 12 f ( 2 5 ) = 14 + 5 5 12 f ( 7 ) = 74 4
Vậy giá trị nhỏ nhất của f(x) là 14 + 5 5 12 tại x= 2 5
Nên thời gian đi ít nhât là BM= x = 2 5

Đáp án A
Phương pháp: Sử dụng phương pháp hàm số.
Cách giải: Gọi độ dài đoạn MB là x ![]()
Tam giác ABM vuông tại B => ![]()
Thời gian người đó đi từ A tới C: 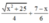
Xét hàm số f(x) 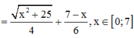

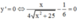
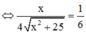
![]()
![]()
=> x = 2 5
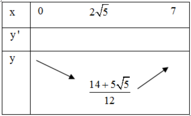
Vậy, để người đó đến C nhanh nhất thì khoảng cách từ B đến M là 2 5

Vận tốc ngược dòng của cano là :
20,5 - 2,2 = 18,3(km/h)
Vận tốc xuôi dòng của thuyền là:
4,5 + 2,2 = 6,7(km/h)
Tổng vận tốc của thuyền và cano là:
18,3 + 6,7 = 25 (km/h)
Thời gian để thuyền gặp cano là ;
42 : 25 = 1,68 (h)
=1 giờ 40 phút 48 giây
Thuyền gặp cano lúc :
8h20' + 1h40'48' =10h48 giây
Chỗ gặp nhau cách B :
6,7 . 1,68 = 11,256 (km)

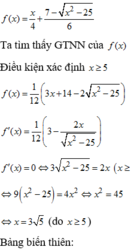
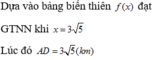

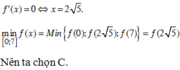
Đáp án D
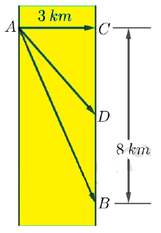
Thời gian đi từ A đến B là t A B = 3 2 + 8 2 6 = 73 6 h .
Thời gian đi từ A đến C rồi đến B là t A C B = 3 6 + 8 8 = 3 2 h
Gọi C D = x k m ⇒ t A D B = x 2 + 9 6 + 8 − x 8 h .
Xét hàm số f x = x 2 + 9 6 + 8 − x 8 0 ≤ x ≤ 8
f ' x = x 6 x 2 + 9 − 1 8 ⇒ f ' x = 0 ⇔ x = 9 7 .
Suy ra f 0 = 3 2 = t A C B , f 8 = 73 6 = t A B , f 9 7 = 1 + 7 8 .
Suy ra thời gian ngắn nhất bằng 1 + 7 8 h .