Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi C là góc tạo bởi đường bay vs mặt đất, AB là độ cao 3200m và B là vị trí của máy bay
Đổi: \(200km/h=\dfrac{500}{9}m/s\)
Xét tam giác ABC vuông tại A:
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{3200}{sin32^0}\approx6038,66\left(m\right)\)
\(t=\dfrac{S}{v}=\dfrac{6038,66}{\dfrac{500}{9}}\approx109\left(s\right)\)

Theo đề bài ta có hình vẽ:
(tự vẽ hình.Gợi ý: )
AC:chiều cao máy bay
BC:quãng đường máy bay
Ta có:AC=10.42=420m
Xét ΔABC vuông tại A có:
⇒\(\sin B\)=\(\dfrac{CA}{BC}\)=\(\dfrac{210}{420}\)=30\(^o\)
vậy máy bay đã tạo môt góc 30 độ.

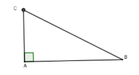
Đổi 1,5’ = 1 40 h
Sau 1,5 phút máy bay ở C
Quãng đường bay được là BC = 480. = 12km và B ^ = 25 0
Nên AC = BC. sin 25 0 = 5,1km
Vậy máy bay đạt được độ cao là 5,1km sau 1,5 phút
Đáp án cần chọn là: C

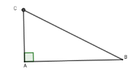
Đổi 1,2’ = 1 50 h
Sau 1,2 phút máy bay ở C
Quãng đường bay được là BC = 500. 1 50 = 10km và B ^ = 30 0
Nên AC = BC. sin 30 0 = 5km
Vậy máy bay đạt được độ cao là 5km sau 1,2 phút
Đáp án cần chọn là: B

Trong 2 phút, máy bay đi được: \(\frac{220.2}{60}=\frac{22}{3}\left(km\right)\)
Gọi mặt đất là AB, độ cao so với mặt đất sau 2 phút là AC, quãng đường máy bay đi được trong 2 phút là AC (theo hình vẽ)
Ta có: \(AC=BC.\sin ABC=\frac{22}{3}.\sin23^o\approx2,865\left(km\right)\)
Vậy máy bay ở độ cao 2,865 km so với mặt đất.
Đổi 3200m = 3,2km
Để đạt đến độ cao 3,2km thì máy bay phải bay \(\dfrac{3,2}{\sin32^0}\approx6\left(km\right)\)
Vậy sau \(6:200=0,03\left(h\right)=1,8\left(giây\right)\) thì máy bay bay đc 3,2km
3200m = 3,2km
Để đạt đến độ cao 3,2km thì máy bay phải bay
Vậy sau thì máy bay bay đc 3,2km