Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
Do mẩu gỗ bị nước dính ướt hoàn toàn, nên lực căng bề mặt ![]() tác dụng lên mẩu gỗ hướng thẳng đứng xuống dưới. Điều kiện để mẩu gỗ nổi trên mặt nước là tổng của trọng lực
tác dụng lên mẩu gỗ hướng thẳng đứng xuống dưới. Điều kiện để mẩu gỗ nổi trên mặt nước là tổng của trọng lực ![]() và lực căng bề mặt
và lực căng bề mặt ![]() phải cân bằng với lực đẩy Ác-si-mét
phải cân bằng với lực đẩy Ác-si-mét ![]() (hình vẽ):
(hình vẽ):
→ P + fc = FA
Gọi a là độ dài mỗi cạnh của mẩu gỗ, x là độ ngập sâu trong nước của mẩu gỗ.
Thay P = mg, fc = σ4a và FA = ρa2xg (bằng trọng lượng nước bị phần mẩu gỗ chìm trong nước chiếm chỗ), ta được: mg + σ.4a = ρ.a2.x.g
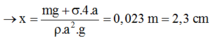
Như vậy lực dính ướt có tác dụng làm mẩu gỗ chìm sâu thêm 0,1 cm chiếm tỉ lệ khoảng hơn 4% độ ngập sâu của mẩu gỗ.

Muốn chiếc kim nổi trên mặt nước thì hiệu số giữa trọng lượng P và lực đẩy Ác-si-mét F A tác dụng lên chiếc kim phải lớn hơn hoặc bằng lực căng bề mặt F c của phần mặt nước đỡ chiếc kim nổi trên nó (H.37.2G) :
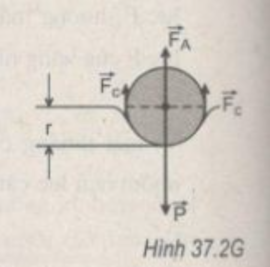
P – F A > F c
Gọi d là bán kính, l là chiều dài và D là khối lượng riêng của chiếc kim, còn D 0 và σ là khối lượng riêng và hệ số căng bề mặt của nước.
![]()
và F A = D 0 .1/2. π d 2 /4 . lg (trọng lượng nước bị một nửa phần chiếc kim chìm trong nước chiếm chỗ), đổng thời chú ý rằng d = 0,05l hay l = 20d, ta tìm được :
![]()
Từ đó suy ra :
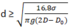
Thay số, ta được :


Đáp án: A
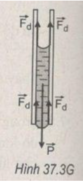
Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt fc của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (hình vẽ).
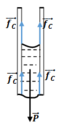
Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt fc đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt Fc của nước.
Fd = Fc = σ.π.d
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước.
Trọng lượng của cột nước:
P = mg = ρghπd2/4
Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là:
P = 2Fd
⇒ ρ.g.h.π.d2/4 = 2σ.π.d
Từ đó suy ra:
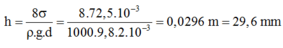

Cột nước còn đọng lại được trong ống mao dẫn là do tác dụng cân bằng giữa trọng lượng P của cột nước với tổng các lực dính ướt F d của thành ống tạo thành mặt khum lõm ở đầu trên và mặt khum lồi ở đầu dưới của cột nước (H.37.3G). Tại vị trí tiếp xúc giữa hai mặt khum của cột nước với thành ống, các lực dính ướt F d đều hướng thẳng đứng lên phía trên và có cùng độ lớn với lực căng bề mặt F c của nước.
F d = F c = σ π d
với d là đường kính của ống mao dẫn và σ là hệ số căng bề mặt của nước. Nếu gọi D là khối lượng riêng của nước và h là độ cao của cột nước trong ống thì trọng lượng cột nước bằng :
P = mg = Dgh π d 2 /4
Khi đó điều kiện cân bằng của cột nước đọng lại trong ống là :
P = 2 F d ⇒ Dgh d 2 /4 = 2 σ π d
Từ đó suy ra :
![]()

Đáp án: D
Lực căng bề mặt của màng xà phòng (có hai mặt) tác dụng lên đoạn dây ab có độ dài l là:
F = 2σ.l
Trọng lượng đoạn dây ab:
P = m.g = V.ρ.g = π.d2.l.ρ.g/4.
Điều kiện cân bằng của dây ab là:
P = F
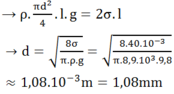

Chọn B
Ta có F m s = μP = μmg
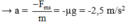
Áp dụng công thức độc lập thời gian có v 2 – v 0 2 = 2aS
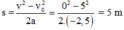
Ta có v = v 0 + at → Thời gian mẫu gỗ chuyển động:
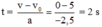

Chọn B.
Ta có F m s = μ N = μ m g (xe chuyển động ngang không có lực kéo nên N = P = mg)
→ xe chuyển động chậm dần đều với gia tốc:


Chọn B.
Ta có Fms = µN = µmg (xe chuyển động ngang không có lực kéo nên N = P = mg)
→ xe chuyển động chậm dần đều với gia tốc: a = - F m s m = - μ g = - 2 . 5 m / s 2
Áp dụng công thức độc lập thời gian có V 2 – V 0 2 = 2aS
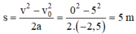
Ta có v = v 0 + at → Thời gian mẫu gỗ chuyển động: t = v - v 0 a = 0 - 5 - 2 . 5 = 2 S
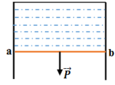
Do mẩu gỗ bị nước dính ướt hoàn toàn, nên lực căng bề mặt F c tác dụng lên mẩu gỗ hướng thẳng đứng xuống dưới. Điều kiện để mẩu gỗ nổi trên mặt nước là tổng của trọng lực P p và lực căng bề mặt F c phải cân bằng với lực đẩy Ác-si-mét F A (H.37.1G):
P + Fc = FA
Gọi a là độ dài mỗi cạnh của mẩu gỗ, x là độ ngập sâu trong nước của mẩu gỗ, D và σ là khối lượng riêng và hệ số căng bề mặt của nước. Thay P = mg, F c = σ 4a và F A = D a 2 xg (bằng trọng lượng nước bị phần mẩu gỗ chìm trong nước chiếm chỗ), ta tìm được:
Thay số:
Như vậy lực dính ướt có tác dụng làm mẩu gỗ chìm sâu thêm 0,1 cm chiếm tỉ lệ khoảng hơn 4% độ ngập sâu của mẩu gỗ.