Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đầu tiên, người thợ gấp đôi tấm vải \(2\) lần liên tiếp, tạo thành \(4\) phần vải rồi đánh dấu
Diện tích \(1\) phần vải là :
\(\dfrac{4}{3}:4=\dfrac{1}{3}\left(m^2\right)\)
\(1m^2\) gấp \(\dfrac{1}{3}m^2\) số lần là :
\(1:\dfrac{1}{3}=3\) (lần)
Vậy người thợ lấy \(3\) phần vải đã dc đánh dấu
~ Chúc bn học tốt ~

Người thợ đó gấp đôi mảnh vải chia thành 2 phần, sau đó tiếp tục gấp đôi manh vải của mỗi mãnh vai trên chia thành 4 phần . Bây giờ người thợ đó cắt \(\dfrac{3}{4}\) mảnh vải dựa theo 4 phần đã chia thì ta có 1 mảnh vải có diện tích 1m\(^2\).

Chào bạn, bạn hãy theo dõi bài giải của mình nhé!
Giải.
Đầu tiên, người thợ gấp đôi miếng vải 2 lần liên tiếp, tạo thành 4 phần vải rồi đánh dấu.
Diện tích 1 phần vải là :
\(\frac{4}{3}:4=\frac{1}{3}\left(m^2\right)\)
1m2 gấp \(\frac{1}{3}m^2\) số lần là :
\(1:\frac{1}{3}=3\)(lần)
Vậy người thợ lấy 3 phần vải đã được đánh dấu.
Chúc bạn học tốt!

Đầu tiên, ta gấp mảnh vải đó thành 4 phần bằng nhau.
Diện tích mỗi phần là:
\(\dfrac{4}{3}:4=\dfrac{1}{3}\left(m^2\right)\)
\(1\) so với \(\dfrac{1}{3}\) thì gấp:
\(1:\dfrac{1}{3}=3\)(lần)
Vậy, sau khi gấp mảnh vải đó thành 4 phần bằng nhau thì ta cắt 3 phần bằng nhau.

Câu 1: Gập mảnh vải thành 4 phần bằng nhau rồi cắt đi một phần.

Đáp án D
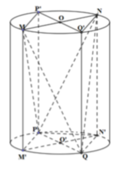
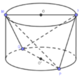
Phương pháp:Thể tích của lượng đá bị cắt bỏ bằng thể tích của khối hình trụ ban đầu trừ đi thể tích của khối tứ diện MNPQ.
Cách giải:
Dựng hình hộp chữ nhật MQ'NP'.M'QN'P như hình vẽ bên.

![]()
![]()
![]()
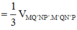
![]()
Hình chữ nhật MQ'NP' có hai đường chéo P’Q’, MN vuông góc với nhau => MO’NP’ là hình vuông
Ta có MN = 60cm = 6dm

Diện tích đáy: ![]()

Thể tích khối trụ:
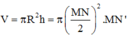

Thể tích của lượng đá bị cắt bỏ: ![]()

Chọn A.
Phương pháp:

Dựng hình lăng trụ MP’NQ’.M’PN’Q (như hình vẽ)
Khi đó, ta có:


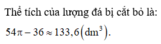

Gấp tấm vải thành 4 phần bằng nhau , sau đó cắt đi 1 phần thì tấm vải sẽ là \(\frac{3}{3}\) , vậy
\(\frac{3}{3}\) là 1m
Gập mảnh vải thành 4 phần bằng nhau , cắt 1 phần còn lại 3 phần.Lấy 3 phần đó lại gập thành 4 phần cắt 3 phần được mảnh vải 1 m2