

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




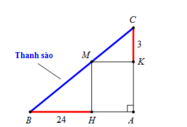
Theo bài ra, thanh sào sẽ đi qua các điểm B, M , C (hình vẽ dưới)
Suy ra độ dài thanh sào là 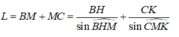
Đặt ![]() ,do đó
L
=
24
sin
x
+
3
cos
x
,do đó
L
=
24
sin
x
+
3
cos
x
Yêu cầu bài toán ⇔ L m i n ⇔ f ( x ) = 24 sin x + 3 cos x m i n
Ta có f ' ( x ) = 3 sin x cos 2 x - 24 cos x sin 2 x = 0 ⇔ sin 3 x = 8 cos 3 x ⇔ tan x = 2 ⇒ cos x = 1 1 + tan 2 x = 1 5 ⇒ sin x = 1 - cos 2 x = 2 5
Suy ra m i n ( 0 ; π 2 ) f ( x ) = 15 5 . Vậy độ dài tối thiểu của thanh sào là 15 5
Chọn C.

Chiều dài là:
\(\left(\dfrac{11}{3}+\dfrac{1}{2}\right):2=\dfrac{25}{12}\left(dm\right)\)
Chiều rộng là:
\(\dfrac{25}{12}-\dfrac{1}{2}=\dfrac{19}{12}\left(dm\right)\)

cần phải tính diện tich đáy
r = d/2 = (98-2)/3,14 = 30,6/2 = 15,3cm
Sday = 3,14.(15,3)2 = 735cm2
V = s.h = 735.30 = 22050cm3=22lít
thùng đựng tối đa 22lít, ố ố la la ta làm dc toán 12
Hô hô người đâu mà cute zo :v cậu 2k mấy dị cho mình xin fb :)))

Đáp án B
Phương pháp:
Trải tất cả các mặt của hình hộp chữ nhật ra cùng một mặt phẳng.
Cách giải:
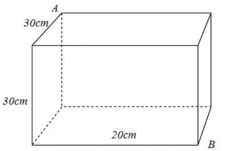
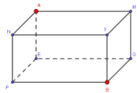

Để đến được B, đầu tiên con kiến phải đi trên một trong các mặt bên và đi đến một trong các cạnh bên: NP, PE, QE, MQ, MF, NF
* Giả sử con kiến đi đến I trên cạnh MF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài
![]()
* Giả sử con kiến đi đến I trên cạnh NF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài
![]()
* Giả sử con kiến đi đến I trên cạnh PF sau đó tới B, khi đó để độ dài quãng đường là ngắn nhất thì A, I, B thẳng hàng:
Độ dài
![]()
Vậy, quãng đường ngắn nhất con kiến đi là 10 34 c m