Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
![]()
Xác suất cần tìm:
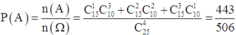

Chọn D
Gọi A là biến cố “4 học sinh được gọi có cả nam và nữ”, suy ra A ¯ là biến cố “4 học sinh được gọi toàn là nam hoặc toàn là nữ”
Số phần tử của không gian mẫu là ![]()
Ta có ![]()
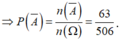
Vậy xác suất của biến cố A là
![]()

Không gian mẫu: \(C_{12}^3\)
a. Số cách chọn 3 học viên đều khá: \(C_5^3\)
Xác suất: \(P=\dfrac{C_5^3}{C_{12}^3}=...\)
b. Số cách chọn sao cho không có học viên khá nào: \(C_7^3\)
\(\Rightarrow\) Số cách chọn có ít nhất 1 học viên khá: \(C_{12}^3-C_7^3\)
Xác suất: \(P=\dfrac{C_{12}^3-C_7^3}{C_{12}^3}\)

n(Ω) = \(C_{40}^4=91390\)
Kí hiệu A : "giáo viên gặp được lớp trưởng "
B : " giáo viên gặp được bí thư chi đoàn"
C : " giáo viên gặp được thủ quỹ "
D : " giáo viên gặp được lớp phó "
=> P(A) = P(B) = P(C) = P(D) = \(\dfrac{C_4^1}{C_{40}^4}\) ~ 0,00004
a) Cần tính \(P\left(A\cap B\right)\) = P(A) . P(B) = 0,000042
b) Cần tính \(P\left(\left(A\cap D\right)\cup\left(A\cap C\right)\right)\\ =P\left(A\cap D\right)+P\left(A\cap C\right)-P\left(A\cap D\right).P\left(A\cap C\right)\\ =P\left(A\right).P\left(D\right)+P\left(C\right).P\left(A\right)-P\left(A\right).P\left(D\right).P\left(A\right).P\left(C\right)\\ =2P^2\left(A\right)-P^4\left(A\right)\\ \)
c) cần tính \(P\left(A\right).P\left(B\right).P\left(D\right).\left(1-P\left(C\right)\right)\)

a) Xác suất để có 2 sinh viên thi đậu:
\(0,6.0,7.0,2+0,6.0,3.0,8+0,4.0,7.0,8=0,452\)
b) Xác suất để có 2 sinh viên thi đậu trong đó sinh viên II không thi đậu:
\(0,6.0,3.0,8=0,144\)