Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

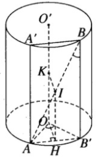
Góc giữa hai bán kính đáy OA và O’B là ∠ AOB′ và ∠ A′O′B
Vì AB’ = r nên AOB’ là tam giác đều , do đó ∠ AOB′=60 °

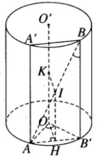
Mặt phẳng (ABB’) chứa AB và song song với trục OO’ của hình trụ. Gọi H là trung điểm của AB’. Ta có OH ⊥ (ABB′). Đường thẳng qua H song song với OO’ cắt AB tại I. Dựng IK // HO cắt OO’ tại K. Ta chứng minh được IK là đoạn vuông góc chung của AB và OO’.
Ta có: IK = HO = 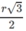

Theo công thức ta có:
Sxq = 2πrh = 2√3 πr2
Stp = 2πrh + 2πr2 = 2√3 πr2 + 2 πr2 = 2(√3 + 1)πr2 ( đơn vị thể tích)
b) Vtrụ = πR2h = √3 π r3
c) Giả sử trục của hình trụ là O1O2 và A nằm trên đường tròn tâm O1, B nằm trên đường tròn tâm O2; I là trung điểm của O1O2, J là trung điểm cảu AB. Khi đó IJ là đường vuông góc chung của O1O2 và AB. Hạ BB1 vuông góc với đáy, J1 là hình chiếu vuông góc của J xuống đáy.
Ta có là trung điểm của
,
= IJ.
Theo giả thiết = 300.
do vậy: AB1 = BB1.tan 300 = = r.
Xét tam giác vuông
AB1 = BB1.tan 300 = O1J1A vuông tại J1, ta có: =
-
.
Vậy khoảng cách giữa AB và O1O2 :

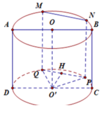
Với O'H = 4 là khoảng cách từ trục đến thiết diện và OO' = h = 8; O'P = O'Q = rd = 6
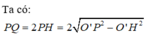
![]() ''
''
Khi đó:
![]()

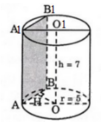
Mặt phẳng (P) song song với trục và cách trục 3cm, cắt hình trụ theo thiết diện là tứ giác A A 1 B 1 B .
Gọi H là trung điểm của AB.
Ta có 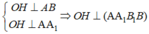

SAA1B1B = AB. AA1 = 8. 7 = 56 (cm2)

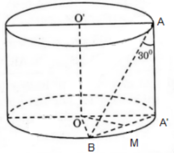

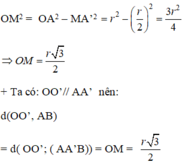

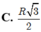
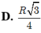

Từ A và B dựng các đường sinh AA’ và BB’ ta có thiết diện qua AB và song song với trục là hình chữ nhật AA’BB’. Góc giữa AB và trục chính là góc ∠ ABB′ . Do đó ∠ ABB′ = 30 ° . Vậy
Do đó diện tích tứ giác AA’BB’ là S AA ' BB ' = AB′. BB′ = r.r 3 = r 2 3