Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ba bi khác màu nên phải chọn từ mỗi hộp 1 viên bi.
Chọn từ hộp thứ ba 1 viên: có 4 cách chọn.
Chọn từ hộp thứ hai 1 viên có số khác với viên bi đã chọn từ hộp ba: có 4 cách chọn
Chọn từ hộp thứ nhất 1 viên bi có số khác với số của hai viên đã chọn từ hộp một và hai: có 4 cách chọn.
Vậy Ω A = 4 3 = 64 .
Đáp án B

Đáp án A
Sắp xếp các viên bi thành ba hàng lần lượt là hàng 1 gồm 4 viên vi vàng đánh số từ 1 đến 4; hàng 2 gồm các 5 viên bi đỏ đánh số từ 1 đến 5, hàng 3 gồm 6 viên bi xanh đánh số từ 1 đến 6 (đóng thẳng cột như hình vẽ).

Việc lựa chọn tiến hành theo ba bước sau:
Bước 1: Chọn 1 viên bi vàng ở hàng thứ nhất: có 4 cách thực hiện.
Sau đó ta xóa đi cột chứa viên bi vàng vừa được chọn.
Bước 2: Chọn 1 viên bi đỏ từ hàng thứ hai từ 4 viên bi đỏ còn lại (1 viên bi đỏ bị loại bỏ sau bước thứ nhất): có 4 cách thực hiện.
Sau đó ta tiếp tục xóa cột chứa viên bi đỏ vừa được chọn.
Bước 3: Chọn 1 viên bi xanh từ 4 viên bi xanh còn lại ở hàng thứ ba: có 4 cách chọn.
Vậy theo quy tắc nhân, có: ![]() cách chọn thỏa mãn
cách chọn thỏa mãn

Có \(C_{24}^3\) cách chọn 3 viên bất kì.
Có \(C_8^3+C_6^3+C_{10}^3\) cách họn 3 viên bi cùng màu.
Có 6 cách chọn 3 viên bi cùng số.
\(\Rightarrow\) Có \(C_{24}^3-\left(C_8^3+C_6^3+C_{10}^3\right)-6=1822\) cách chọn 3 viên bi khác màu, khác số.
Chọn 1 viên xanh: có 6 cách
Chọn 1 viên đỏ khác số viên xanh: 7 cách
Chọn 1 viên vàng khác số viên xanh và đỏ: 8 cách
Tổng cộng: \(6.7.8=336\) cách

Chọn D
Chọn ngẫu nhiên 4 viên bi từ hộp có 12 viên bi thì có ![]()
Số cách lấy để được đủ ba màu là ![]()
Xác suất để 4 viên bi lấy ra có đủ ba màu bằng
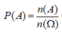
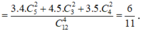

Gọi A là biến cố: “trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
Trong hộp có tất cả: 5+ 15 + 35 = 55 viên bi
- Số phần tử của không gian mẫu: Ω = C 55 7 .
- A ¯ là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào.”
=> n A ¯ = C 20 7 .
Vì A và A ¯ là hai biến cố đối nên: n A = Ω − n A ¯ = C 55 7 − C 20 7 .
Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là P A = C 55 7 − C 20 7 C 55 7 .
Chọn đáp án B.

Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có
![]()
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là
n(X) = 3.4.5 = 60
![]()

Không gian mẫu: \(C_{15}^4\)
a.
Số cách lấy 4 viên bi trong đó có 3 viên màu đỏ: \(C_7^3C_8^1\)
Xác suất: \(P=\dfrac{C_7^3.C_8^1}{C_{15}^4}\)
b.
Lấy 4 viên không có viên đỏ nào (lấy từ 8 viên 2 màu còn lại): \(C_8^4\) cách
Lấy 4 viên có ít nhất 1 viên đỏ: \(C_{15}^4-C_8^4\)
Xác suất: \(P=\dfrac{C_{15}^4-C_8^4}{C_{15}^4}\)
c.
Các trường hợp thỏa mãn: (2 đỏ 1 xanh 1 vàng), (1 đỏ 2 xanh 1 vàng), (1 đỏ 1 vàng 2 xanh)
Số cách lấy: \(C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2\)
Xác suất: \(P=\dfrac{C_7^2C_5^1C_3^1+C_7^1C_5^2C_3^1+C_7^1C_5^1C_3^2}{C_{15}^4}\)

a. Mỗi viên bi đánh một số, nên 2 viên bi lấy ra mang số khác nhau. Vậy
Ω={(m,n)|1≤n≤7 và m≠n}
Chọn B
Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi.
Suy ra số phần tử của không gian mẫu là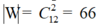 .
.
Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số .
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4=16 cách (do số bi đỏ ít hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh).
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4=12cách.
● Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3=9 cách.
Suy ra số phần tử của biến cố A là 16+12+9=37.
Vậy xác suất cần tính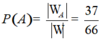 .
.
Chọn B.