Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi diện tích trồng đậu là x ( đơn vị là a, 0 < x < 8).
Diện tích trồng cà là: 8 - x (a).
Tổng số tiền thu được là: \(3000000x+4000000\left(8-x\right)=32000000-1000000x\).
Tổng số công cần là: \(20x+30\left(8-x\right)=240-10x\).
Theo yêu cầu của đề bài: \(240-10x\le180\)\(\Leftrightarrow10x\ge60\)\(\Leftrightarrow x\ge6\).
Mặt khác \(x\le8\) nên \(6\le x\le8\).
Ta cần \(32000000-1000000x\) đạt giá trị lớn nhất nên \(x=6\).
Vậy diện tích trồng đậu 6a, diện tích trồng cà là 2a thì số tiền thu được lớn nhất bằng: \(32000000-1000000.6=26000000\) đồng.
Diện tích khu đất hình vuông có trồng chè và cà phê là:
3x3=9(km2)
Diện tích trồng chè là:
9:(2+1)x1=3(km2)
Diện tích trồng cà phê là:
9 - 3 = 6 (km2)
Đáp số: 3 (km2)
diện tích khu đất hunhf chữ nhật là:
3.3=9(km2)
diện tích trồng chè là:
9:(2+1)=3(km2)
diện tích trồng cà phê là:
9-3=6(km2)
Đáp số: diện tích trồng chè là 3km2
diện tích trồng cà phê là 6km2
Chọn B
Gọi x; y lần lượt là số cái bánh đậu xanh, bánh dẻo . Khi đó; số tiền lãi là L= 2x+ 1,8 y
Bài toán trở thành tìm số tự nhiên x; y thoả mãn hệ
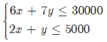sao cho L= 2x+ 1,8 y lớn nhất.
Từ đó ta có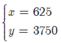 
thì L đạt giá trị lớn nhất.
Vậy cần 625 bánh đậu xanh và 3750 bánh dẻo thì lãi lớn nhất.
Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m 2 ), điều kiện x ≥ 0, y ≥ 0, ta có x + y ≤ 0
Số công cần dùng là 20x + 30y ≤ 180 hay 20 + 3y ≤ 18
Số tiền thu được là
F = 3000000x + 4000000y (đồng)
Hay F = 3x + 4y (đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình
Sao cho F = 3x + 4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x = 6, y = 2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6a đậu, 2a cà, thu hoạch 26 000 000 đồng.