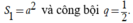Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Phương pháp:
Nếu u n là một cấp số nhân với công bội q ≠ 1 thì S n được tính theo công thức: S n = u 1 1 − q n 1 − q .
Cách giải:
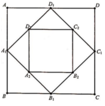
Hình vuông ABCD cạnh a ⇒ S 1 = a 2
Hình vuông A 1 B 1 C 1 D 1 có cạnh bằng a 2 ⇒ S 2 = a 2 2
Hình vuông A 2 B 2 C 2 D 2 có cạnh bằng
a 2 2 = a 2 2 ⇒ S 3 = a 2 2 2
……
Hình vuông A 99 B 99 C 99 D 99 có cạnh bằng a 2 99 ⇒ S 100 = a 2 2 99
S = S 1 + S 2 + S 3 + ... + S 100 = a 2 2 0 + a 2 2 1 + a 2 2 2 + ... + a 2 2 99 = a 2 . 1 − 1 2 100 1 − 1 2 = a 2 2 100 − 1 2 100 .2 = a 2 2 100 − 1 2 99

Đáp án C
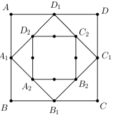
Diện tích hình vuông A B C D là S 1 = a 2 ; diện tích hình vuông A 1 B 1 C 1 D 1 là S 2 = a 2 2 2 = a 2 2
Diện tích hình vuông A 2 B 2 C 2 D 2 là a 2 2 = a 2 4 ; ...
Diện tích hình vuông A 99 B 99 C 99 D 99 là S 100 = a 2 2 99
Vậy S = a 2 1 2 0 + 1 2 1 + 1 2 2 + ... + 1 2 99 ⏟ T
với T là tổng của CSN có u 1 = 1 ; q = 1 2 và n = 100
Do đó, tổng:
S = a 2 . 1 − 1 2 100 1 − 1 2 = 2 a 2 1 − 1 2 100 = a 2 2 100 − 1 2 99

Đáp án B.
Ta có V = a b c S = 2 a b + b c + c a . Theo đề ta có:
a b c = 2 a b + b c + c a ; 1 ≤ a ≤ b ≤ c ⇔ 1 = 2. a b + b c + c a a b c ⇔ 2 a + 2 b + 2 c = 1
Ta có 1 = 2 a + 2 b + 2 c ≤ 2 a + 2 a + 2 a = 6 a ⇒ a ≤ 6 . Kết hợp với 2 a + 2 b + 2 c = 1 ta có:
a = 3 ⇒ 1 b + 1 c = 1 6 ⇒ 6 < b ≤ 12
⇒ a ; b ; c e { 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 }
Với a = 4 ⇒ 1 b + 1 c = 1 4 ⇒ 4 < b ≤ 8 ⇒ a ; b ; c ∈ 4 ; 5 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8
với a = 5 ⇒ 1 b + 1 c = 3 10 < 1 3 ⇒ b < 6 ⇒ a ; b ; c ∈ 5 ; 5 ; 10
với a = 6 ⇒ 1 b + 1 c = 1 3 ⇒ b ≤ 6 ⇒ a ; b ; c ∈ 6 ; 6 ; 6
⇒ a ; b ; c ∈ 3 ; 7 ; 42 , 3 ; 8 ; 24 , 3 ; 9 ; 18 , 3 ; 10 ; 15 , 3 ; 12 ; 12 4 ; 6 ; 20 , 4 ; 6 ; 12 , 4 ; 8 ; 8 , 5 ; 5 ; 10 , 6 ; 6 ; 6
Vậy ta chọn B.

Chọn A

Phương pháp:
Cách giải:


Mà AH vuông góc (BCD) nên AH là trục của mặt phẳng (BCD).
Gọi K là trung điểm AD, kẻ OK vuông góc với AD, O thuộc AH







Ta tính được
Như vậy S 1 , S 2 , S 3 , . . . , S 100 là cấp số nhân với