Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu.


Nguyễn Thị Thu Hà thật là oai oai oai học giỏi mà bài tổng và hiệu cũng hỏi người khác

a.có 18 HLP nhỏ có mặt được sơn xanh,1 HLP nhỏ có 1 mặt sơn xanh
b.có 24 HLP nhỏ được sơn đỏ ,có 12 HLP nhỏ đc sơn đỏ 2 mặt,12 HLP nhỏ đc sơn đỏ 1 mặt
c. có 3 HLP nhỏ không đc sơn mặt nào
tích mình nhé :D thanks

Chọn A.
Phương pháp
Ta sử dụng công thức diện tích hình chiếu
S
'
=
S
.
cos
α
Với S là diện tích hình H , S’ và là diện tích hình chiếu của H trên mặt phẳng (P), α là góc tạo bởi mặt phẳng chứa hình H và mặt phẳng (P).
Cách giải:
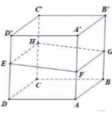

Lại có hình chiếu của EFGH xuống mặt phẳng (ABCD) là hình vuông ABCD cạnh 3
Theo công thức tính diện tích hình chiếu ta có
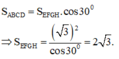

Đáp án D
Phương pháp: Gắn hệ trục tọa độ Oxyz để giải bài toán.
Cách giải: Giả sử mặt phẳng chứa AC’ cắt hình lập phương theo thiết diện là tứ giác AEC’F ![]()
Ta có: 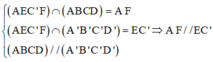
Tương tự ta chứng minh được AE//FC’
=>AEC’ F là hình bình hành ![]()
Gắn hệ trục tọa độ như hình vẽ sao cho A’(0;0;0); B’(2;0;0); C’(2;2;0); D’(0;2;0); A(0;0;2); B(2;0;2); C(2;2;2); D(0;2;2)
Gọi E(x;0;0) (0≤x≤2) ta có:
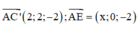
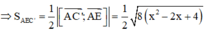
Ta có ![]()
Dấu bằng xảy ra ó x = 1, khi đó ![]()

Đáp án D
Giả sử (P) cắt cạnh AA’ tại M sao cho A'M = x
Chọn hệ trục tọa độ như hình vẽ
B(0;0;1), D'(1;1;0), M(1;0;x)
B D ' → 1 ; 1 ; - 1 , B M → 0 ; - 1 ; x + 1 ⇒ B D ' → , B M → = x ; - x - 1 ; - 1
Thiết diện BMD’N thu được là hình bình hành nên
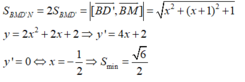
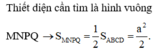


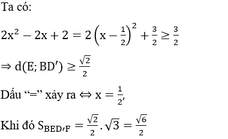
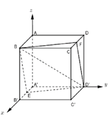
Đáp án C.
Mỗi mặt sẽ có 4 phần thuộc hình chỉ được tô một lần tức là mỗi mặt sẽ sinh ra 4 hình lập phương thỏa mãn yêu cầu bài toán, ta có 6 mặt, từ đó ta có 24 hình thỏa mãn yêu cầu