Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(X \rightarrow Y + \alpha\)
Định luật bảo toàn động năng \(\overrightarrow P_{X} =\overrightarrow P_{Y}+ \overrightarrow P_{\alpha} = \overrightarrow 0. \)
=> \( P_{Y}= P_{\alpha} => m_Y v_Y = m_{\alpha}v_{\alpha}\) hay \(\frac{m_Y}{m_{\alpha}}= \frac{v_{\alpha}}{v_Y}.(1)\)
Lại có \(P^2 = 2mK.\)
=> \(m_YK_Y=m_{\alpha}K_{\alpha}\)
=> \(\frac{m_Y}{m_{\alpha}}= \frac{K_{\alpha}}{K_Y}.(2)\)
Từ (1) và (2) => \(\frac{m_Y}{m_{\alpha}}= \frac{K_{\alpha}}{K_Y} =\frac{v_{\alpha}}{v_Y} .\)

C.
\(T_{1_{ }_{ }}:T_{2_{ }}=\sqrt{\dfrac{m.k_2}{k_1.m}}=\sqrt{\dfrac{k_2}{k_1}}=\dfrac{1}{2}\)
\(\dfrac{k_2}{k_1}=\dfrac{1}{4}\)
\(\Rightarrow\left\{{}\begin{matrix}k_1=4k_2\\k_1+k_2=5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}k_2=1\\k_1=4\end{matrix}\right.\)

Số khối của hạt nhân Y là : A - 4.
Theo định luật bảo toàn động lượng, ta có :
m α V → + m Y V → = 0 → ⇒ 4 v → + A - 4 V → = 0 → ⇒ 4 v → = - A - 4 V →
v là tốc độ của hạt nhân Y.
Về độ lớn, ta có : V = 4v/(A - 4)

1. Hướng dẫn
Hạt $\alpha$ là $^4_2He$, hạt $X$ là \(^{20}_{10}X\)
Áp dụng ĐLBT động lượng
\(\vec{p}=\vec{p_1}+\vec{p_2}\)
\(\Rightarrow p^2=p_1^2+p_2^2+2p_1p_2\cos \varphi\)
\(\Rightarrow mK=m_1K_1+m_2K_2+2\sqrt{m_1m_2K_1K_2}\cos \varphi\)
Lấy $m=1u,m_1=4u,m_2=20u$
$ \Rightarrow \cos \varphi=...$
$ \Rightarrow \varphi=...$
2. Bạn xem ở đây nhé
Câu hỏi của trần thị phương thảo - Vật lý lớp 12 | Học trực tuyến

\(_1^1p + _4^9Be \rightarrow \alpha + _3^6Li\)
Phản ứng này thu năng lượng => \(W_{thu} =(m_s-m_t)c^2 = K_t-K_s\)
=> \( K_p+ K_{Be}-K_{He}- K_{Li} = W_{thu} \) (do Be đứng yên nên KBe = 0)
=> \(K_p = W_{thu}+K_{Li}+K_{He} = 2,125+4+3,575 = 9,7MeV.\)
Áp dụng định luật bảo toàn động lượng
\(\overrightarrow P_{p} =\overrightarrow P_{He} + \overrightarrow P_{Li} \)
Dựa vào hình vẽ ta có
Áp dụng định lí hàm cos trong tam giác
=> \(\cos {\alpha} = \frac{P_p^2+P_{He}^2-P_{Li}^2}{2P_pP_{He}} = \frac{2.1.K_p+ 2.4.K_{He}-2.6.K_{Li}}{2.2.2m_pm_{He}K_pK_{He}} = 0.\)
Với \(P^2 = 2mK, m=A.\).
=> \(\alpha = 90^0.\)
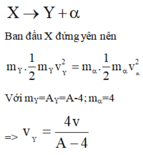
Chọn C