Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Mua 15 vé trong 100 vé có C 100 15 cách ⇒ n Ω = C 100 15
Gọi X là biến cố “người đó trúng 2 vé”
Mua 2 vé trúng trong 5 vé trúng có C 5 2 cách, mua 13 vé còn lại trong 95 vé có C 95 13 cách
Suy ra số kết quả thuận lợi cho biến cố X là n X = C 5 2 . C 95 13
Vậy xác suất cần tính P = n X n Ω = C 5 2 . C 95 13 C 100 15 ≈ 14 %

Không gian mẫu: Ω = C 100 12
Gọi biến cố A là: “Người đó không trúng vé nào”
n A = C 98 12
Xác suất của biến cố A là P A ≈ 77 %

Tập S có tất cả 2 6 = 64 tập con. Mỗi bạn có 64 cách viết ngẫu nhiên. Nên số phần tử không gian mẫu bằng 64 3
Ta tìm số cách viết thoả mãn:
Gọi x, y, z là số phần tử có trong các tập con của A, B, C viết lên bảng.
Vì các tập con của ba bạn này viết khác rỗng nên x , y , z ≥ 1
Vì các tập con của ba bạn này đôi một không giao nhau và trên bảng có đúng 4 phần tử của S nên x+y+z=4
Vậy ta có hệ 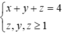
⇔ ( x ; y ; z ) = 1 ; 1 ; 2 ; 1 ; 2 ; 1 ; 2 ; 1 ; 1
Vậy có tất cả ![]() cách viết thoả mãn.
cách viết thoả mãn.
Xác suất cần tính bằng ![]()
Chọn đáp án B.

Đáp án B
Số cách sắp ngẫu nhiên là C 9 3 C 6 3 C 3 3 = 1680 (cách)
Số cách sắp để ba đội của Việt Nam ở 3 bảng khác nhau là: C 6 2 C 3 1 C 4 2 C 2 1 C 2 2 C 1 2 = 540 (cách)
Xác suất để 3 đội bóng của Việt Nam ở 3 bảng khác nhau là: 540 1680 = 9 28

Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.

Số phần tử của không gian mẫu là: n Ω = C 8 4 = 70
Gọi X là biến cố: “cả hai bạn Việt và Nam nằm chung một bảng đấu’
Số kết quả thuận lợi cho biến cố X là: n X = C 2 1 C 2 6 = 30
Vậy xác suất cần tính P X = n X n Ω = 30 70 = 3 7
Đáp án B

Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
![]()
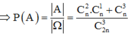
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2


Số cách mua 3 vé ngẫu nhiên C 20000 3 Số cách mua 3 vé trúng 1 giải nhì và 2 giải khuyến khích C 100 1 C 5000 2 Xác suất cần tính bằng
C 100 1 C 5000 2 C 20000 3 ≈ 0 , 00094 = 0 , 094 %
Chọn đáp án C.