Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định luật II-Niuton có: \(\overrightarrow{F_{ms}}+\overrightarrow{P}+\overrightarrow{N}=m\overrightarrow{a}\)
Chiếu các vector lực lên trục ngang ta có:
\(-F_{ms}=ma\Leftrightarrow-500=10.10^3a\Rightarrow a=-0,05\) m/s2
Đổi 36km/h=10m/s
Ta có: \(v^2-v_0^2=2aS\Leftrightarrow0^2-10^2=2.\left(-0,05\right)S\Rightarrow S=1000m\)
Vậy tàu phải dừng cách ga 1000m

Đổi 54km/h = 15m/s; 1p = 60s
Gia tốc của tàu là:
Ta có: \(v=v_0+at\Leftrightarrow a=\dfrac{v-v_0}{t}=\dfrac{0-15}{60}=-0,25\left(m/s^2\right)\)

Quãng đường mà tàu đi đi được trong thời gian hãm phanh là:
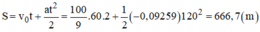

Đổi: 36km/h=10m/s; 18km/h=5m/s
Ta có: v=v0+at
⇔5=10+a.20⇔a=−0,25(\(\dfrac{m}{s^2}\))
Ta lại có: v=v0+at
⇔0=10−0,25t⇔t=40(s)
\(v_0=36\)km/h=10m/s
\(v=18\)km/h=5m/s
Gia tốc vật:
\(v=v_0+at\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{5-10}{20}=-0,25\)m/s2
Thời gian tàu đi từ lúc hãm phanh đến khi dừng lại\(\left(v'=0\right)\):
\(v'=v+at\Rightarrow t=\dfrac{v'-v}{a}=\dfrac{0-5}{-0,25}=20s\)

Giải: Chọn chiều dương là chiều chuyển động của tàu, gốc tọa độ tại vị trí hãm phanh, gốc thời gian lúc bắt đầu hãm phanh.
a. v 0 = 72 3 , 6 = 20 m / s ; v 1 = 54 3 , 6 = 15 m / s ; v 2 = 36 3 , 6 = 10 m / s
gia tốc chuyển động của tàu a = v 1 − v 0 Δ t = 15 − 20 10 = − 0 , 5 m / s 2
Mà v 2 = v 0 + a . t 2 ⇒ t 2 = v 2 − v 0 a = 10 − 20 − 0 , 5 = 20 s
Khi dừng lại hẳn thì v 3 = 0
Áp dụng công thức v 3 = v 0 + a t 3 ⇒ t 3 = v 3 − v 0 a = 0 − 20 − 0 , 5 = 40 s
b;Áp dụng công thức v 3 2 − v 0 2 = 2. a . S ⇒ S = v 3 2 − v 0 2 2. a = 400 m
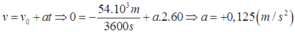


Chọn đáp án B
? Lời giải:
+ Khi tắt máy, gia tốc của đầu tàu là