NQ
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
2 tháng 10 2017
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc trong của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4680
ó = 4680 - 3600
ó = 1080
ó 1800.n – 3600 = 1080 .n
ó 1800.n – 1080 .n = 3600
ó 720.n = 3600
ó n = 3600: 720
ó n = 5
Vậy đa giác đề cần tìm có 5 cạnh.
Đáp án cần chọn là: A
CM
10 tháng 7 2018
Gọi n là số cạnh của đa giác đều cần tìm (n ≥ 3)
Mỗi góc của đa giác đều có số đo
( n − 2 ) 180 ° n
Tổng số đo các góc ngoài của một đa giác là 3600
Theo bài ra ta có phương trình:
3600 + ( n − 2 ) 180 ° n = 4800
ó = 4800 - 3600
ó = 1200
ó 1800.n – 3600 = 1200 .n
ó 1800.n – 1200 .n = 3600
ó 600.n = 3600
ó n = 3600: 600
ó n = 6
Vậy đa giác đề cần tìm có 6 cạnh.
Đáp án cần chọn là: C
3 tháng 9 2021
Số đường chéo của đa giác đều n cạnh là \(\dfrac{n\left(n-3\right)}{2}\)
Số đường chéo bằng 33 số cạnh
\(\Rightarrow\dfrac{n\left(n-3\right)}{2}=33n\Rightarrow n\left(n-3\right)=66n\\
\Rightarrow n-3=66\\
\Rightarrow n=69\)
Suy ra đa giác đều đó có 69 cạnh
Số đo mỗi góc là \(\dfrac{180\cdot33+360}{69}\approx91,3\)
TL
3
20 tháng 9 2019
Gọi số cạnh là n
Ta có công thức tính mỗi góc của đa giác đều n cạnh là :
\(\frac{\left(n-2\right).180^0}{n}\)
CC
20 tháng 9 2019
Đa giác đều có số đường chéo bằng số cạnh
\(\Rightarrow\)Đa giác đều đó là tam giác đều và tổng số đo mỗi góc là \(60^o\)
CM
27 tháng 9 2019
Tổng số đo các góc ngoài của đa giác bằng 360 0
Số đo một góc trong của đa giác đều là 468 0 – 360 0 = 108 0
Gọi n là số cạnh của đa giác đều. Ta có số đo mỗi góc của đa giác đều bằng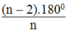 
Suy ra: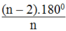
=
108
0
⇒ 180.n – 360 = 108.n⇒ 72n = 360⇒ n = 5
Vậy đa giác đều cần tìm có 5 cạnh.
26 tháng 4 2017
a) Tổng số đo các góc của một đa giác n cạnh = \((7-2).180^0\) = \(900^0\)
b)Số đo mỗi góc của ngũ giác đều là : \(\frac{(5-2).180^0}{5}\)= \(108^0\)
Số đo mỗi góc của lục giác đều là \(\frac{(6-2).180^0}{6}\)= \(120^0\)
1 tháng 7 2017
ta có công thức sô đo 1 góc của đa giác là \(\frac{180\left(n-2\right)}{n}\)=168
nên số cạnh là n=30
số đường chéo theo công thức \(\frac{n\left(n-3\right)}{2}\)=30.27:2=405
PT
1
CM
2 tháng 10 2019
Hướng dẫn:
+ Số đo của một góc của đa giác đều n cạnh là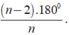
Khi đó số đo của một góc của đa giác đều 20 cạnh là:
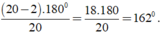
+ Số đường chéo của đa giác n cạnh là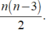
Khi đó số đường chéo của đa giác đều 20 cạnh là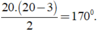
Gọi số cạnh của tam giác là n
Ta có: \(\frac{\left(n-2\right).180^0}{n}=156^0\)
\(\Leftrightarrow\left(n-2\right).180^0=156^0n\)
\(\Leftrightarrow180^0n-360^0=156^0n\)
\(\Leftrightarrow180^0n-156^0n=360^0\)
\(\Leftrightarrow24^0n=360^0\)
\(\Leftrightarrow n=15\)
Vậy đa giác đó có 15 cạnh