Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

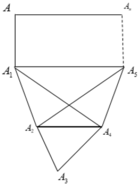
Nhận thấy: Hình vuông và hình ngũ giác đều thỏa mãn yêu cầu của bài toán
Ta chứng minh đa giác có số cạnh lớn hơn 5 không thỏa mãn yêu cầu của bài toán bằng phương pháp phản chứng.

là các cạnh của tứ giác nên tổng hai đường chéo lớn hơn tổng hai cạnh đối.

⇒ Giả thiết đưa ra là sai.
Vậy đa giác có số cạnh lớn hơn 5 thì không thỏa mãn yêu cầu bài.

gọi \(z,y,z\text{ là các cạnh của tam giác vuông ,ta có}\)
\(x^2+y^2=z^2\left(1\right)\)
\(xy=2\left(x+y+z\right)\left(2\right)\)
\(\text{Từ (1) ta có:}\)
\(z^2=\left(z+y\right)^2-2xy=\left(x+y\right)^2-4\left(x+y+z\right)\Rightarrow\left(x+y\right)^2-4\left(x+y\right)+4=z^2-4z+4\)
\(\Rightarrow\left(x+y-2\right)^2=\left(z+2\right)^2\)
\(\Rightarrow x+y-2=z+2\left(x+y\ge2\right)\)
Thay z=x+y−4vào (2) ta được :
\(\left(x-4\right)\left(y-4\right)=8\)
\(\Leftrightarrow x-4=1;y-4=8\)hoặc \(x-4=2;y-4=4\)
\(\Leftrightarrow x=5;y=12\)hoặc \(x=6;y=8\)
