Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng công thức: \(l=R\alpha\).
a) \(l=25.\dfrac{3\pi}{7}=\dfrac{75\pi}{7}\) (cm).
b) Đổi \(49^o=\dfrac{49\pi}{180}\).
\(l=25.\dfrac{49\pi}{180}\left(cm\right)=\dfrac{245}{36}cm\).
c) \(l=25.\dfrac{4}{3}\left(cm\right)=\dfrac{100}{3}cm\).

chu vi hình tròn là P=\(\partial R\)\(\Pi\)=10
\(\dfrac{3\pi}{4}=135^o\Rightarrow\) độ dài của \(\dfrac{3\pi}{4}\) là 10 : 360 x 135 = \(\dfrac{15}{4}\)

Để tính độ dài l của một cung có số đo α radian trên đường tròn bán kính R ta áp dụng công thức: l = Rα
Đổi số đo 20 ο thành radian ta được: 20 x 0,0175 = 0,35.
Với bán kính R = 36/2 = 18 ta có độ dài l là: 18 x 0,35 = 6,3 (cm).
Đáp án: D

Chọn B.
Độ dài của cung 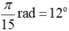 trên đường tròn được tính bằng công thức:
trên đường tròn được tính bằng công thức:
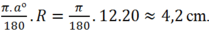
A
bn này luôn là đầu