Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Lô 1 : Xác suất lấy sản phẩm tốt : 0,6
Xác suất lấy sản phẩm không tốt : 0,4
Lô 2 : Xác suất lấy sản phẩm tốt :0,7
Xác suất lấy sản phẩm không tốt : 0,3
⇒ xác suất để trong hai sản phẩm lấy ra có ít nhất một sản phẩm có chất lượng tốt :
p = 0 , 6.0 , 7 + 0 , 6.0 , 3 + 0 , 7.0 , 4 = 0 , 88

Gọi C là chi phí mỗi ngày. Khi đó C = 16m + 27n(USD)
Do hàm sản xuất phải đạt chỉ tiêu 40 sản phẩm trong mỗi ngày nên
m 2 3 b 1 3 ≥ 40 ⇔ m 2 n ≥ 40 3 ⇔ n ≥ 40 3 m 3
Biểu thức biểu diễn mối liên hệ giữa số lượng nhân viên và chi phí kinh doanh là
C ≥ 16 m + 27 . 40 3 m 2
Áp dụng bất đẳng thức Cauchy ta có
C ≥ 16 m + 27 . 40 3 m 2 = 8 m + 8 m + 27 . 40 3 m 2 ≥ 1440
Vậy C = 1400 (USD) khi và chỉ khi
8 m = 27 . 40 3 m 2 n = 40 3 m 2 ⇔ m = 60 n = 18
(có 60 nhân viên và lao động xấp xỉ 18 người)
Đáp án B

+) Gọi số ngày mà xí nghiệp đã hoàn thành công việc là x (x>0, ngày )
- Theo dự định, trong một ngày, xí nghiệp sản xuất đựoc số sản phẩm là 1500 : 30 = 50 (sản phẩm )
-Trên thực tế, trong một ngày, xí nghiệp sản xuất được số sản phẩm là 50 + 15 = 65 ( sản phẩm )
+) Theo đề bài ta có phương trình :
65x = 1500 + 255
<=> 65x = 1755
<=> x =1755 : 65 =27 (ngày )
=> Thực tế, xí nghiệp đã rút ngắn được số ngày là 30 - 27 = 3(ngày)
dự định 1 ngày làm đc : 1500 : 30 = 50sp
thực tế 1 ngày làm đc 50+15=65 sp
gọi số ngày làm thực tế là x (ngày) x>0
ta có số sp thực tế làm đc là 65x
=> 65x = 1500+255
<=> x = 27
thực tế xí nghiẹp đã rút ngắn đc 3 ngày

Đáp án B
Gọi A là biến cố: “ 3 sản phẩm lấy ra có ít nhất một sản phẩm tốt”
Khi đó A ¯ là biến cố :”3 sản phẩm lấy ra không có sản phẩm nào tốt”
Ta có:
Ω = C 10 3 ; Ω A = C 10 3 ⇒ P A ¯ = C 10 3 C 30 3 = 6 203
Suy ra
P A = 1 − P A ¯ = 197 203 .

Đáp án C
n Ω = C 40 3
A : ‘ 3 sản phẩm lấy ra có ít nhất 1 sản phẩm tốt ‘
A ¯ : ‘3 sản phẩm lấy ra không có sản phẩm tốt ‘
n A ¯ = C 10 3 P ( A ) = 1 − P ( A ¯ ) = 1 − C 10 3 C 40 3 = 244 247

Chọn B


Vậy để thu được lợi nhuận cao nhất thì cần sản xuất 20 sản phẩm loại I và 40 sản phẩm loại II


Số phần trăm chỉ số gạo ngày thứ ba bán được là:
100% - 30% - 38% = 32% (cả 3 ngày)
Ngày thứ 3 của hàng bán được:
2500 x 32% = 800 (kg)
Đáp số: 800 kg gạo
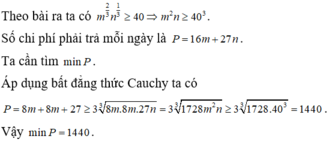
Số sản phẩm bán được ở ngày 1,2,3,.... lập thành cấp số nhân với u 1 = 5 , q = 2. Theo giả thiết ta có: