Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
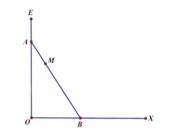
Gọi M x 0 ; y 0 ∈ C ⇒ y ' x 0 = 3 x 0 2 - 3 và y x 0 = x 0 3 - 3 x 0 .
Suy ra phương trình tiếp tuyến của (C) tại M là y = y x 0 = y ' x 0 . x - x 0 .
⇔ y = 3 x 0 2 - 3 . x - x 0 + x 0 3 - 3 x 0 = 3 x 0 2 - 3 . x - 2 x 0 3 ( d ) .
Phương trình hoành độ giao điểm của (C) và (d) là x 3 - 3 x = 3 x 0 2 - 3 x - 2 x 0 3
⇔ x 3 - 3 x 0 2 . x + 2 x 0 3 = 0 ⇔ x - x 0 2 x + 2 x 0 = 0 ⇔ [ x = x 0 x = - 2 x 0 .
Vậy x M = x 0 x N = - 2 x 0 ⇒ 2 x M + x N = 0 .

Đáp án D
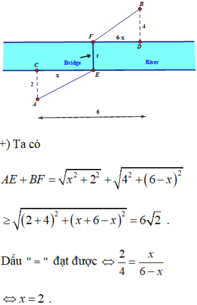
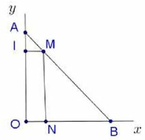
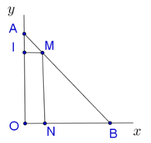
Gọi A B O ^ = α ( 0 < α < 90 0 ) thì ta dễ dàng thấy được
A B = 1 s i n α + 1 8 cos α k m .
Đặt t = sin α ta có A B = f t = 1 t + 1 8 1 − t 2 với t ∈ 0 ; 1
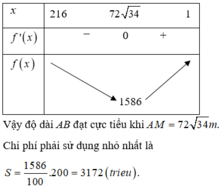
Ta có f ' t = − 1 t 2 + t 8 t 2 − 1 t 2 − 1 ; f ' t = 0 ⇔ t = 2 5 . Khi đó dùng bảng biến thiên dễ thấy min A B = f 2 5 = 5 5 8 ⇒ chi phis thấp nhất là 5 5 8 .1,5 = 2,0963 tỉ đồng.

Đáp án C
Phương pháp: Xác định các đường tiệm cận của đồ thị hàm số.
Gọi điểm M thuộc đồ thị hàm số (C), tính khoảng cách từ M đến các đường tiệm cận và sử dụng BĐT Cauchy tìm GTNN của biểu thức đó từ đó suy ra tọa độ các điểm M, N.
Tính độ dài MN.
Cách giải: TXĐ: D = R\ {3}
Đồ thị hàm số có đường TCN y = 4 (d1) và TCĐ x = 3 (d2).
Gọi điểm M
∈
(C) có dạng 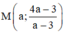 khi đó ta có:
khi đó ta có:
![]()
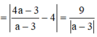
![]()
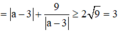
Dấu = xảy ra

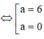
![]()

Đáp án B
Phương pháp:
Giả sử khối lượng công việc đã làm được trong 1 tháng đầu là x thì tổng khối lượng công việc là 24x.
Giả sử sau n tháng thì xong công trình, tính khối lượng công việc sẽ hoàn thành sau n tháng.
Cách giải:
Giả sử khối lượng công việc đã làm được trong 1 tháng đầu là x thì tổng khối lượng công việc là 24x.
Giả sử sau n tháng thì xong công trình, ta có phương trình
x + 1 , 04 x + 1 , 04 2 x + ... + 1 , 04 n − 1 x = 24 x ⇔ 1 , 04 n − 1 1 , 04 − 1 = 24 ⇔ n = 17 , 16
Vậy công trình sẽ hoàn thành ở tháng thứ 18
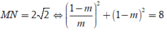
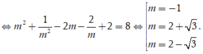







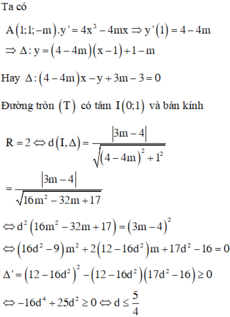
Theo quy tắc nhân có mn cách.
Chọn đáp án C.