Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
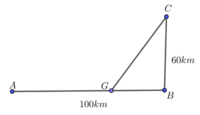
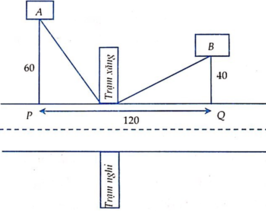
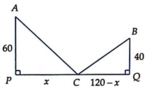
Đặt GB = x (km), 0 < x < 100 ![]() Số tiền cần để mắc dây điện từ đến rồi từ G đến E là:
Số tiền cần để mắc dây điện từ đến rồi từ G đến E là:
![]() (triệu đồng)
(triệu đồng)
Cách 1:
![]()
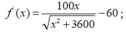
![]()
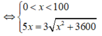
⇔ x = 45
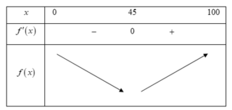
Vậy f(x) đạt giá trị nhỏ nhất tại x = 45 => GA = 55km.
Cách 2: Dùng casio sử dụng MODE 7 được đạt giá trị nhỏ nhất tại x = 45 => GA = 55 km.

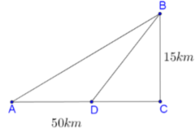
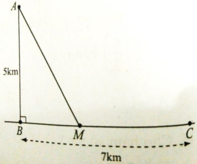
Đặt BM = x (0 ≤ x ≤ 7) => MC = 7 - x. Áp dụng định lí Py-ta-go cho tam giác vuông ABM có
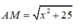
Thời gian đi từ A đến M là
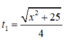
thời gian đi từ M đến C là
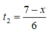
Tổng thời gian đi từ A đến C là
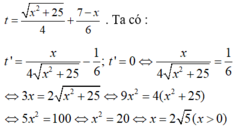
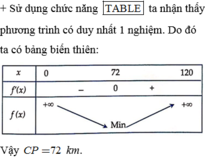
Bảng biến thiên
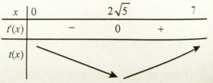
Để người đó đến kho nhanh nhất thì thời gian đi cần ít nhất, tức t đạt giá trị nhỏ nhất. Dựa vào bảng biến thiên ta thấy t đạt giá trị nhỏ nhất tại x = 2√5 ≈ 4,5
Vậy vị trí điểm M cách B một khoảng là 4,5km thì người đó đến kho là nhanh nhất.
Chọn B

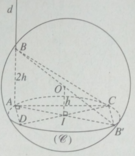
Diện tích tam giác BCD bằng:
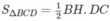
Diện tích này lớn nhất khi AI // CD.

Gọi quãng được A đi được là x thì quãng đường B đi được là 177-x
A đi hết quãng đường trong 7h nên: v1 = x/7
B đi hết quãng đường trong 4h nên: v2 = (177-x)/4
B đi với vận tốc lớn hơn A là 3km/h nê: v2 = v1 + 3
(177-x)/4 = x/7 +3
x = 105
v1 = 15 ; v2 = 18


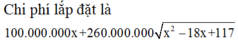
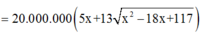

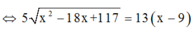
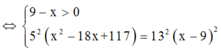



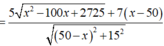


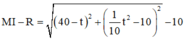
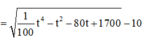
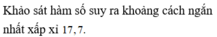

À rồi, nếu mình hiểu không nhầm thì có nghĩa là \(BB'=6(km)\)
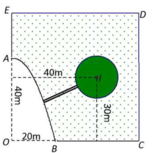
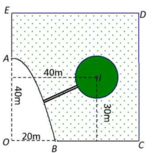
Theo đề bài: Xét tam giác vuông tại $B'$ là $AB'B$ có điểm $M\in AB'$
Đặt $MB'=x$. Chi phí đường ống là: \(AM.5000+13000MB=5000(9-x)+13000\sqrt{36+x^2}\)
Để chi phí min thì \(y=13000\sqrt{36+x^2}-5000x\) phải min.
Có \(y'=\frac{13000x}{\sqrt{36+x^2}}-5000=0\Leftrightarrow x=\pm 2,5\). Do đó $y$ min khi $x=2,5$, tức là $AM=9-2,5=6,5$
Do đó $D$ là đáp án đúng.
Một công ty muốn chạy một đường ống dẫn từ một điểm A trên bờ đến một điểm B trên một hòn đảo mà là 6 km từ bờ biển
Câu bôi đậm có nghĩa gì vậy bạn =)))