Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C.
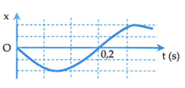
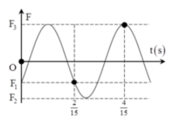
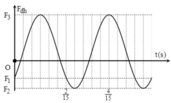
Từ đồ thị ta có chu kỳ dao động của vật là T = 0 , 4 s
Độ cứng của lò xo là k = m ω 2 = m 2 π T 2 = 123 N / m

Giải thích: Đáp án A
Phương pháp: Sử dụng lí thuyết về lực đàn hồi cực đại, cực tiểu trong dao động của con lắc lò xo thẳng đứng
Cách giải:
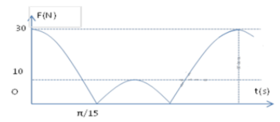
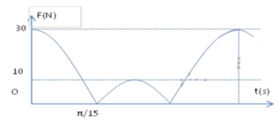
Từ đồ thị ta có:
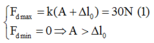
+ Lực đàn hồi khi vật nặng ở vị trí cao nhất là: Fđh = k ( A - Dl0 ) =10N (2)
ỞThời gian từ khi lực đàn hồi của lò xo đạt giá trị cực đại đến khi lực đàn hồi của lò xo đạt giá trị cực tiểu (vị trí lò xo tự nhiên) là π/15 s
Từ (1) và (2) ta có: 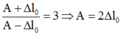
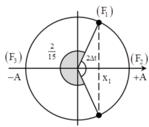
Dùng đường tròn lượng giác:

Ta có 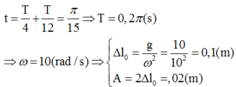
Thay vào (1) ta có: 
Khối lượng vật nặng: 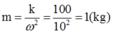

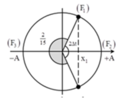
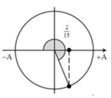
Lực đàn hồi của lò xo được xác định bằng biểu thức F = - k ( ∆ l 0 + x ) với ∆ l 0 là độ biến dạng của lò xo tại vị trí cân bằng và x là li độ của vật.
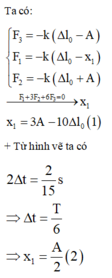
Từ (1) và (2) ta tìm được
∆ l 0 = 0 , 25 A
+ Tỉ số giữa thời gian lò xo giãn và nén trong một chu kì là
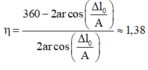
Đáp án B

Đáp án A
Phương pháp: Sử dụng lí thuyết về dao động điều hòa kết hợp với kĩ năng đọc đồ thị
Cách giải :
Tần số góc: ω = k m
Từ đồ thị ta có:
+ Biên độ dao động A = 8cm
+ t = 0 vật đi qua vị trí x = 4cm theo chiều dương => φ = - π/3(rad)
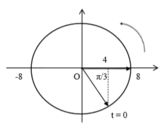
=> PT dao động của vật: x = 8cos(10t - π/3) cm=> Chọn A

Chọn đáp án A
@ Lời giải:
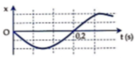
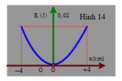
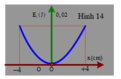
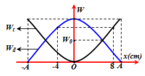
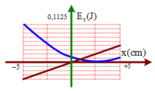
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → E h d = m g x → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
E d h = 0 , 5 k ( Δ l 0 – x ) 2 → ứng với đường nét liền.
+ Từ đồ thị, ta có: x m a x = A = 5 c m ; E d h m a x = m g A ↔ 0 , 05 = m . 10 . 0 , 05 → m = 0,1 kg.
E d h m a x = 0 , 5 k ( Δ l + A ) 2 ↔ 0 , 1125 = 0 , 5 . k ( 0 , 025 + 0 , 05 ) 2 → k = 40 N/m.
+ Khi vật đi qua vị trí lò xo không biến dạng → x = Δ l 0 = 0 , 5 A = 2 , 5 c m .
→ v = 3 2 v m a x = 3 2 40 0 , 1 .5 = 86 , 6 cm/s.
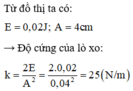


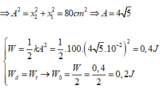


Đáp án C
Từ đồ thị ta có chu kỳ dao động của vật là T=0,4s
Độ cứng của lò xo là