Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Trong quá trình dao động của vật điểm treo vừa bị kéo và ném
![]()
Ta có
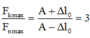
![]()
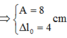
Vận tốc cực đại của vật
![]()
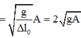
![]()

Chọn D
+ F nmax = k(A - Dl) = 2 (1)
+ Fkmax = k(A + Dl) = 4 (2)
+ Lập tỉ số (1) và (2) ta được: A = 3Dl
+ Mà ∆ l = mg k = 1 ω 2 g ® A = 3 1 ω 2 g ® ω 2 A = a max = 3g = 30 m/ s 2 .

Đáp án C
Áp dụng ĐLBTĐL và ĐLBTNL
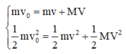
Từ 2 pt trên tìm được
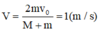
Ta thấy độ giảm năng lượng của vật ở VTCB ban đầu và vị trí lò xo nén cực đại chính là công của lực ma sát
Suy ra
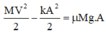
![]()
![]()
Khi vật chuyển động từ vị trí lò xo nén cực đại về lại VTCB, lực ma sát sinh ra sẽ khiến VTCB bị lệch về phía lò xo nén 1 lượng
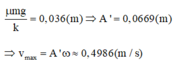

Đáp án D
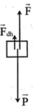
+ Trọng lực của quả cầu: ![]()
+ Ta có: P>F nên muốn quả cầu nằm cân bằng thì
F
đh
khi đó phải có chiều hướng lên và có độ lớn thỏa mãn: ![]()
+ Độ giãn của lò xo tại vị trí bắt đầu thả vật: ![]()
+ Độ giãn của lò xo tại VTCB: 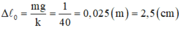
+ Từ hình bên ta có: ![]()
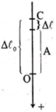
+ Lực đàn hồi cực đại tác dụng lên giá treo:
![]()
+ Do ∆ l 0 >A nên lực đàn hồi cực tiểu:
![]()

Đáp án D
Chu kì dao động của con lắc lò xo:
Độ dãn của lò xo ở VTCB
Vì ban đầu ta đưa vật dọc theo trục lò xo đến vị trí lò xo không biến dạng rồi buông nhẹ cho vật dao động điều hòa
→ biên độ dao động A = 10 cm
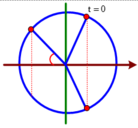
Lực đàn hồi cuẩ lò xo có độ lớn cực đại ở vị trí biên dương và lực đàn hồi của lò xo có độ lớn bằng nửa giá trị cực đại và đang giảm khi vật ở x = 0 và đang đi theo chiều âm.
Từ hình vẽ suy ra t = T/2 + T/4 = 0,47s


Vì lực kéo về luôn hướng về VTCB O, lực đàn hồi luôn hướng về TN (vị trí lò xo có độ dài tự nhiên) nên để 2 lực này ngược chiều nhau, vật phải di chuyển trên đoạn giữa O và TN. 1 chu kỳ vật đi qua đoạn này 2 lần nên suy ra thời gian đi qua đoạn này là T/6
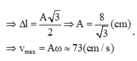


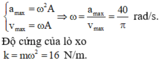
Đáp án A
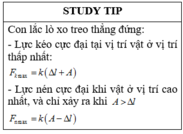
Ta có lực kéo đại được tính bởi công thức F k max = k Δ l + A
Và nén cực đại được tính bởi công thức F n max = k A − Δ l
Thay số ta có 4 = 50 Δ l + A 2 = 50 − Δ l + A ⇒ độ biến dạng của lò xo Δ l = 2 c m và biên độ dao động A = 6 (cm)
Từ hệ quả của định luật Húc m . g = k . Δ l , ta có tần số của dao động: ω = g Δ l = 500 r a d / s
Như vậy tần số góc của dao động v max = ω A = 60 5 c m