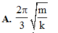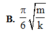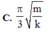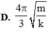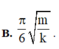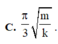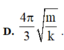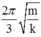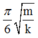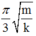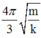Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong quá trình dao động của vật, lò xo bị nén → A > Δl0.
Ta có
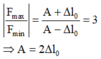
Vậy thời gian lò xo bị nén trong một chu kì là
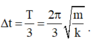
Đáp án A

Giải thích: Đáp án A
Phương pháp: Công thức tính lực đàn hồi ![]()
Cách giải :
Trong quá trình dao động của vật lò xo bị nén ![]()
Ta có 
Vậy thời gian lò xo bị nén trong một chu kì là 

Chọn A
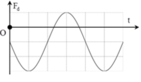
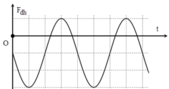
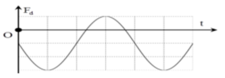
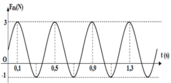
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
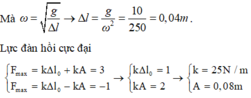
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.

Đáp án D
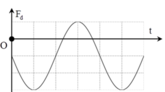
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
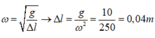
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 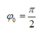 rad.
rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm

Đáp án D
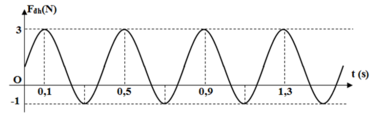
Độ giãn của con lắc ở vị trí cân bằng: T = 0,4 s = 2 π ∆ l 0 g ⇒ ∆ l 0 = T 2 g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
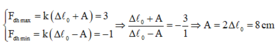
Độ cứng của lò xo: k = F d h m a x ∆ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
![]()
Tại thời điểm t = 0,1 s , lực đàn hồi có giá trị F = 3N nên:
F d h = 1 + 2 cos ( 5 π . 0 , 1 + μ ) = 3
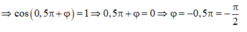
Phương trình dao động của vật: x = 8 cos ( 5 πt - π 2 ) ( c m )

Chọn đáp án A
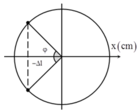
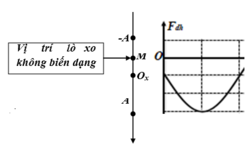
Vì lò xo treo thẳng đứng và có thời gian bị nén nên A > Dl.
Thời gian lực kéo về ngược chiều với lực đàn hồi ứng với vật dao động từ vị trí cân bằng đến vị trí lò xo không biến dạng (tại A) và từ B về VTCB.
→t = 2/15 = (2.(90⁰-j))/ꞷ (1)
Thời gian lò xo bị nén ứng với vật dao động từ A đến B.
→t = 2/15 = 2j/ꞷ (2)
Từ (1) và (2) ® j = 300 ® w = 5p rad/s ® T = 0,4 s
w = g ∆ l = 5p → ∆ l = 0,04m = 4cm
cosj = ∆ l /A→A= ∆ l /cosj = 4/cos30⁰ = 8/ 3 cm

- Vì lò xo treo thẳng đứng và có thời gian bị nén nên A > Δl.
- Thời gian lực kéo về ngược chiều với lực đàn hồi ứng với vật dao động từ vị trí cân bằng đến vị trí lò xo không biến dạng (tại A) và từ B về VTCB.
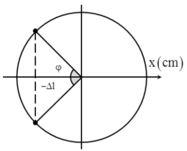
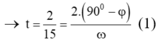
Thời gian lò xo bị nén ứng với vật dao động từ A đến B:
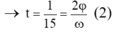
- Từ (1) và (2):